第三章:滤波与褶积,Z变换
约 1628 字大约 5 分钟
2026-01-29
注
本章系统介绍数字信号处理中最核心的操作之一——滤波,从频域与时间域两个角度阐明其原理,并引入褶积作为滤波的时间域实现方式。进一步,通过引入Z变换,将离散信号频谱简化为代数形式,为后续系统分析(如线性时不变系统、递归滤波器设计等)奠定数学工具基础。
§1 连续信号的滤波与褶积
1. 滤波问题的提出
实际信号 x(t) 通常包含有效信号 s(t) 与干扰信号 n(t)
x(t)=s(t)+n(t)
若 s(t) 与 n(t) 的频谱 S(f),N(f) 分离(即 S(f)N(f)≡0),则可设计滤波器频谱 H(f)
H(f)={1,0,S(f)=0S(f)=0
使得输出 Y(f)=H(f)X(f)=S(f),即完全消噪、保留有效信号。
滤波便是将原始信号 x(t) 的频谱 X(f) 与滤波器频谱 H(f) 相乘,得输出频谱 Y(f)=X(f)H(f) 的过程。一般情形下,S(f) 与 N(f) 重叠但特性不同,仍可依频谱差异设计 H(f),实现削弱干扰、增强信号的目的。
2. 连续信号的滤波与褶积
设输入信号为 x(t),滤波器频谱为 H(f),对应时间函数为 h(t),输出频谱为 Y(f)=X(f)H(f),对应时间函数为 y(t)。
通过傅里叶逆变换与积分交换顺序,可得
y(t)=∫−∞∞h(τ)x(t−τ)dτ
此即 褶积(或卷积)运算,记为
y(t)=x(t)∗h(t)
§2 离散信号的滤波与褶积
1. 离散信号的滤波与褶积
对抽样间隔为 Δ 的离散信号 x(nΔ),滤波因子 h(nΔ),其频谱分别为 XΔ(f),HΔ(f)。若 x(t),h(t) 均有截频 fc,且抽样满足 1/(2Δ)≥fc,则离散滤波可精确实现连续滤波。
离散滤波关系为:
YΔ(f)=XΔ(f)HΔ(f)
对应时域关系(褶积)为:
y(nΔ)=Δτ=−∞∑∞h(τΔ)x((n−τ)Δ)
记为:
y(nΔ)=x(nΔ)∗h(nΔ)
2. 褶积的直观意义
将离散褶积改写为:
y(nΔ)=Δτ=−∞∑∞h(−τΔ)x((n+τ)Δ)
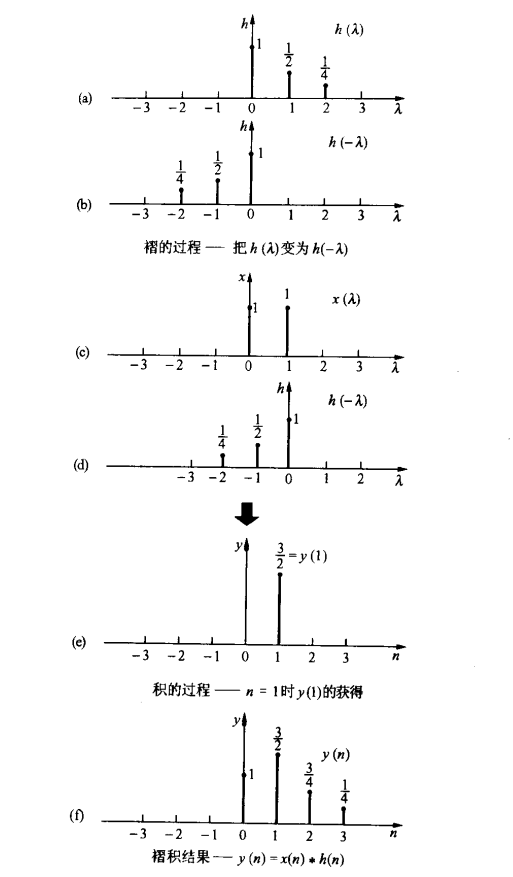
几何解释:
- 将 h(⋅) 作翻褶(h(τ)→h(−τ))
- 将翻褶后的 h(−τ) 与 x(τ) 对齐于 n 处
- 逐点相乘并求和(乘积累加),即得 y(nΔ)
- 移动对齐点 n→n+1,重复即可得整个输出序列
此即“褶而后积”名称来源:先翻褶,再对应相乘累加。
§3 信号的能谱与能量等式,功率谱与平均功率等式
1. 连续信号的能谱与能量等式
信号能量定义为:
E=∫−∞+∞x2(t)dt
若 x(t) 频谱为 X(f),则有能量等式(Parseval 等式):
∫−∞∞x2(t)dt=∫−∞∞∣X(f)∣2df
∣X(f)∣2 称为 x(t) 的能谱。
2. 连续信号的功率谱与平均功率等式
若信号能量无限(如周期信号、平稳随机信号),则研究平均功率:
P=T→∞lim2T1∫−TTx2(t)dt
其功率谱定义为:
G(f)=T→∞lim2T1∫−TTx(t)e−i2πftdt2
对应平均功率等式:
P=∫−∞∞G(f)df
3. 离散信号的能谱与能量等式
离散信号 x(nΔ) 的能量为:
E=Δn=−∞∑∞∣x(nΔ)∣2
其频谱为 XΔ(f),则离散能量等式为:
Δn=−∞∑∞∣x(nΔ)∣2=∫−1/(2Δ)1/(2Δ)∣XΔ(f)∣2df
∣XΔ(f)∣2 为离散信号的能谱。
4. 离散信号的功率谱与平均功率等式
离散信号平均功率定义为:
P=N→∞lim2N+11n=−N∑N∣x(nΔ)∣2
其功率谱为:
G(f)=N→∞lim(2N+1)Δ1n=−N∑Nx(nΔ)e−i2πnΔf2
满足平均功率等式:
P=∫−1/(2Δ)1/(2Δ)G(f)df
§4 离散信号与频谱的简化表示
为简化记号与计算,引入以下简化约定:
以 xn 表示 x(nΔ)
定义三种频谱形式(取决于变量选择):
类型 频谱表达式 变量范围 XΔ(f) XΔ(f)=Δ∑nxne−i2πnΔf f∈[−2Δ1,2Δ1] X(f) X(f)=∑nxne−i2πnΔf f∈[−2Δ1,2Δ1] X(ω) X(ω)=∑nxne−inω ω∈[−π,π],其中 ω=2πΔf
能量关系(统一形式):
n=−∞∑∞∣xn∣2=⎩⎨⎧Δ1∫−1/(2Δ)1/(2Δ)∣XΔ(f)∣2dfΔ∫−1/(2Δ)1/(2Δ)∣X(f)∣2df2π1∫−ππ∣X(ω)∣2dω
褶积简化表示:
gn=xn∗hn=τ=−∞∑∞hτxn−τyn=Δg(n)
对应频域为:
G(f)=X(f)H(f),G(ω)=X(ω)H(ω)Y(f)=ΔG(f),Y(ω)=ΔG(ω)
§5 离散信号的 Z 变换
注
将离散信号频谱 X(ω)=∑xne−inω 中的 e−iω 替换为复变量 Z,即得 Z 变换。它将频谱表达转换为幂级数形式,便于代数运算与系统分析。
1. 离散序列的频谱与 Z 变换
设离散序列 xn,定义其 Z 变换为:
X(Z)=n=−∞∑∞xnZn
与频谱关系为:
X(ω)=X(Z)Z=e−iω,X(f)=X(Z)Z=e−i2πΔf
即:Z 变换是频谱的代数化表示,Z 为复变量。
Z 变换基本性质:
| 运算 | 时域 | Z 域 |
|---|---|---|
| 褶积 | yn=xn∗hn | Y(Z)=X(Z)H(Z) |
| 翻转 | gn=x−n | G(Z)=X(Z−1) |
| 相关 | rxy(n)=xn∗y−n | Rxy(Z)=X(Z)Y(Z−1) |
| 自相关 | rxx(n)=xn∗x−n | Rxx(Z)=X(Z)X(Z−1) |
| 时移 | xn−t | ZtX(Z) |
2. 频谱与 Z 变换展开式的惟一性
展开式惟一定理:
若离散序列 xn 的频谱或 Z 变换有展开式:
X(ω)=∑cne−inω或X(Z)=∑cnZn
则系数 cn 唯一确定,且 cn=xn。
应用:可直接从 X(Z) 的幂级数展开中读出序列 xn。