第十章:有限长脉冲响应滤波器和窗函数
约 2378 字大约 8 分钟
2026-01-29
注
本章核心:研究理想滤波器的不可实现性及其改进方法;系统介绍窗函数法(含性能分析与设计流程);阐述广义线性相位 FIR 滤波器的四种类型及频谱结构;补充频率抽样法与误差最大最小优化法。
§1 理想滤波器及其存在的问题
1. 理想滤波器
| 滤波器类型 | 频谱H(f)(∣f∣≤2Δ1) | 说明 |
|---|---|---|
| 理想低通 | H1(f)={1,0,∣f∣≤f1f1<∣f∣≤2Δ1 | f1:高通频率 |
| 理想带通 | H2(f)={1,0,f1<∣f∣≤f2其他 | f1:低通频率;f2:高通频率 |
| 理想高通 | H3(f)={0,1,∣f∣≤f1f1<∣f∣≤2Δ1 | f1:高截频率 |
| 理想带阻 | H4(f)={0,1,f1<∣f∣≤f2其他 | f1:低截频率;f2:高截频率 |
| 希尔伯特滤波器 | H5(f)={−i,i,0<f≤2Δ1−2Δ1<f<0 | 用于 90° 相移 |
| 理想微分滤波器 | H6(f)=i2πf | 对应微分运算 |
注
对应的时域脉冲响应
- 理想低通:h1(n)=πnΔsin2πf1nΔ
- 希尔伯特:h5(n)=⎩⎨⎧0,πnΔ1−(−1)n,n=0n=0
- 理想微分:h6(n)=⎩⎨⎧0,nΔ2cosπn,n=0n=0
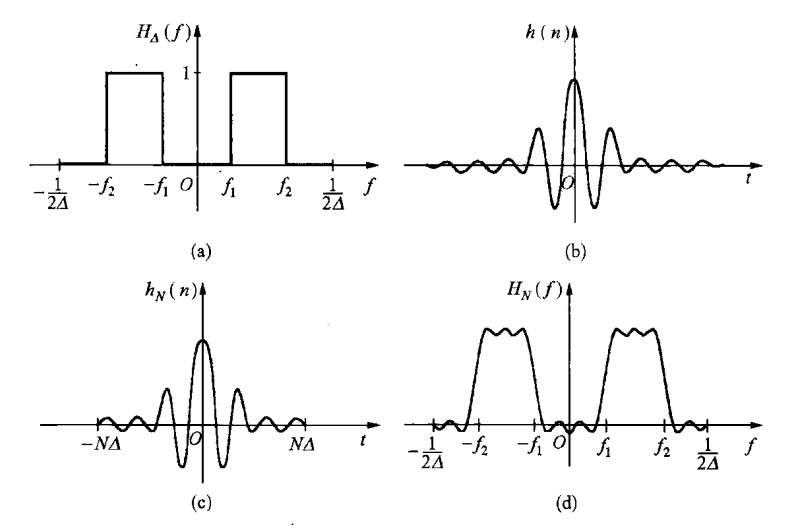
2. 理想滤波器存在的问题
根本问题:理想滤波器的时域脉冲响应 h(n) 无限长。
截尾引起的吉布斯现象:
将 h(n) 截尾为有限长 hN(n)=h(n)⋅gN(n)(gN为矩形窗),其频谱 HN(f) 在理想突变点(如 ±f1)附近产生严重振荡。
3. 近似理想滤波器技术指标(以低通为例)
定义于圆频率 ω=2πΔf 域:
{1−δp≤∣H(ω)∣≤1+δp,∣H(ω)∣≤δs,0≤ω≤ωpωs≤ω≤π
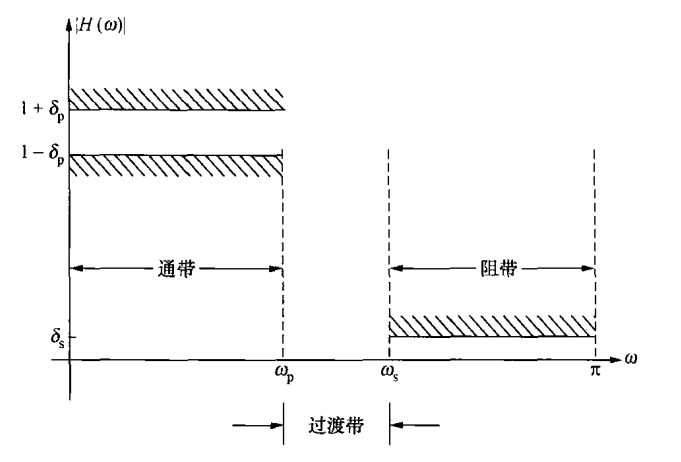
ωp:通带截止频率
ωs:阻带起始频率
δp:通带波动
δs:阻带波动
过渡带:[ωp,ωs],中点21(ωp+ωs)对应理想截频
分贝表示:αp=20lg(1−δp),αs=20lgδs
§2 时窗函数
1. 矩形时窗与截尾效应
矩形时窗:
gN(n)={1,0,∣n∣≤N其他
对应频谱(主瓣+旁瓣):
GN(f)=sinπΔfsin2π(N+21)Δf
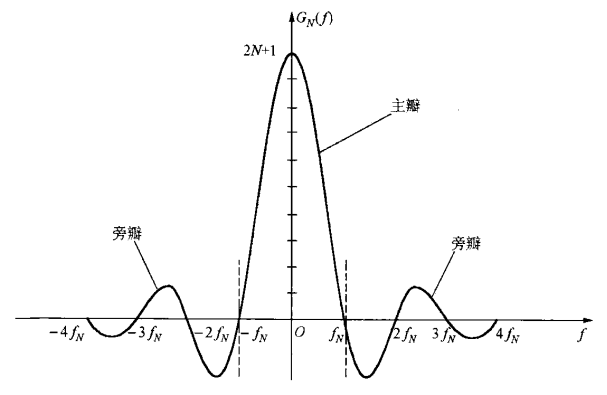
主瓣宽度:2fN=(2N+1)Δ2
吉布斯现象成因:
截尾频谱 XN(f)=X(f)∗GN(f),主瓣使原频谱平滑,旁瓣泄漏引起振荡。
好的时窗函数要求:
- 旁瓣峰值低,减小泄漏效应;
- 主瓣宽度窄,提高频率分辨率。
2. 常用时窗函数
2.1 矩形(Rectangular)时窗
w1(t)=⎩⎨⎧1,0,∣t∣≤T∣t∣>T
W1(f)=πfsin2πfT
2.2 三角形(Bartlett)时窗
w2(t)=⎩⎨⎧1−T∣t∣,0,∣t∣≤T其他
W2(f)=T(πfTsinπfT)2
2.3 钟形(Gauss)时窗
w3(t)=⎩⎨⎧exp[−α(Tt)2],0,∣t∣≤T其他
W3(f)≈απT2e−απ2T4f2
2.4 哈宁(Hanning)时窗
w4(t)=⎩⎨⎧21(1+cosTπt),0,∣t∣≤T其他
W4(f)=21W1(f)+41[W1(f−2T1)+W1(f+2T1)]=2πfsin2πfT+21⋅1−(2Tf)2sin2πfT
2.5 汉明(Hamming)时窗
w5(t)=⎩⎨⎧0.54+0.46cosTπt,0,∣t∣≤T其他
W5(f)=0.54W1(f)+0.23[W1(f−2T1)+W1(f+2T1)]=πfsin2πfT[0.54−1−(2Tf)20.08cos2πfT]
2.6 帕曾(Parzen)时窗
w6(t)=⎩⎨⎧1−6(Tt)2+6Tt3,2(1−T∣t∣)3,0,∣t∣≤2T2T<∣t∣≤T∣t∣>T
W6(f)=43(πfT/2sin(πfT/2))4
2.7 截尾丹尼尔(Truncated Daniell)时窗
w7(t)=⎩⎨⎧πt/Tsin(πt/T),0,∣t∣≤T∣t∣>T
W7(f)=W1(f)∗U(f),其中U(f)=⎩⎨⎧T,0,∣f∣≤2T1∣f∣>2T1
2.8 布拉克曼(Blackman)时窗
w8(t)=⎩⎨⎧0.42+0.5cosTπt+0.08cosT2πt,0,∣t∣≤T其他
W8(f)= 0.42W1(f)+0.25[W1(f−2T1)+W1(f+2T1)]+0.04[W1(f−T1)+W1(f+T1)]
2.9 凯苏(Kaiser)时窗
w9(t)=⎩⎨⎧I0(β)I0(β1−(t/T)2),0,∣t∣≤T∣t∣>T
其中I0为修正的第一类零阶贝塞尔函数,β为形状参数。
W9(f)=⎩⎨⎧I0(β)(2πfT)2−β22Tsin(2πfT)2−β2,I0(β)β2−(2πfT)22Tsinhβ2−(2πfT)2,2π∣f∣T>β2π∣f∣T<β
| 时窗函数 | 旁瓣峰值 (dB) | 过渡带宽度 c | 阻带衰减 (dB) |
|---|---|---|---|
| 矩形 | –13 | 0.9/N | –21 |
| 三角形 | –25 | 2.1/N | –25 |
| 哈宁 | –31 | 3.1/N | –44 |
| 汉明 | –41 | 3.3/N | –53 |
| 布拉克曼 | –57 | 5.5/N | –74 |
注
设计时窗函数步骤:
- 已知滤波器所需技术指标。
- 由 δs 查表选取窗类型。
- 由过渡带宽 Δω=ωs−ωp 和 c=2πΔω 确定 N。
- 取理想滤波器截频为过渡带中点。
- 考虑物理可实现取 N/2 保证因果性;
- 构造 h(n)=hideal(n)⋅w(n)。
3. 最佳时窗函数
3.1 最大振幅比时窗(切比雪夫窗)
设离散时窗 hn=h−n,则频谱 H(f)=∑n=−NNhncos2πnΔf。给定 0<δ<2Δ1,要求 (−δ,δ) 是时窗函数频谱的主瓣范围。
使振幅比
Q(h)=maxδ≤∣f∣≤2Δ1∣H(f)∣H(0)
达最大的时窗函数 wn 称为最大振幅比时窗函数,其频谱对应切比雪夫多项式:
PN(x)=cos[Narccos(a−12x−a−1)]
x=cos2πΔf,a=cos2πδΔ<1
3.2 最大能量比时窗
给定 0<δ<2Δ1,希望 H(f) 的能量集中在区间 (−δ,δ) 内。
定义使能量比
Q(h)=∫−2Δ12Δ1∣H(f)∣2df∫−δδ∣H(f)∣2df
达最大的时窗函数 hn 为最大能量比时窗函数,对应如下特征值问题最大特征根 Q(h) 的特征向量。
n=−N∑Nπ(n−k)Δsin2π(n−k)δΔhn=Q(h)⋅hk,k=−N,…,N
§3 广义线性相位滤波器,有限长脉冲响应滤波器设计的其他方法
1. 广义线性相位有限长脉冲响应滤波器
设有限长物理可实现滤波器:
h(n)={h(n),0,0≤n≤M其他
| 类型 | 对称性 | M 奇偶性 | 频谱 H(e−iω) | 特点 |
|---|---|---|---|---|
| Ⅰ类 | h(n)=h(M−n) | 偶 | e−iωM/2∑k=0M/2a(k)coskω | 广义线性相位,ϕ(ω)=−ωM/2 |
| Ⅱ类 | h(n)=h(M−n) | 奇 | e−iωM/2∑k=1(M+1)/2b(k)cos[(k−21)ω] | 广义线性相位,ω=π 处必为零 |
| Ⅲ类 | h(n)=−h(M−n) | 偶 | ie−iωM/2∑k=1M/2c(k)sinkω | 广义线性相位,ω=0,π 处必为零 |
| Ⅳ类 | h(n)=−h(M−n) | 奇 | ie−iωM/2∑k=1(M+1)/2d(k)sin[(k−21)ω] | 广义线性相位,ω=0 处必为零 |
注
线性相位滤波器:A(e−iω)=∣H(e−iω)∣,ϕ(ω)=−iαω。
广义线性相位滤波器:A(e−iω) 可取负值,ϕ(ω)=−i(αω+β)。
非线性相位滤波器是信号波形产生畸变,因此在设计滤波器时,希望其具有线性相位,或者广义线性相位。
2. 频率抽样法
设理想滤波器频谱为 H(e−jω),取 N 点频率 ωk=N2πk,k=0,1,…,N−1,则根据有限离散傅氏变换,近似 FIR 滤波器为:
hN(n)=N1k=0∑N−1H(e−iωk)eiωkn,0≤n≤N−1
且与原脉冲响应有如下关系:
hN(n)=k=−∞∑∞h(n+kN),0≤n≤N−1
注
优化方法:
- 将主能量部分时移至 [0,N−1]。
- 对频谱镶边使之光滑。
3. 误差最大最小优化法(切比雪夫逼近)
以低通滤波为例,定义加权误差:
E(e−iω)=W(e−iω)[HL(e−iω)−A(e−iω)]
其中
W(e−iω)=⎩⎨⎧δpδs,1,0≤ω≤ωpωs≤ω≤π,HL(e−iω)=⎩⎨⎧1,0,0≤ω≤ωpωs≤ω≤π
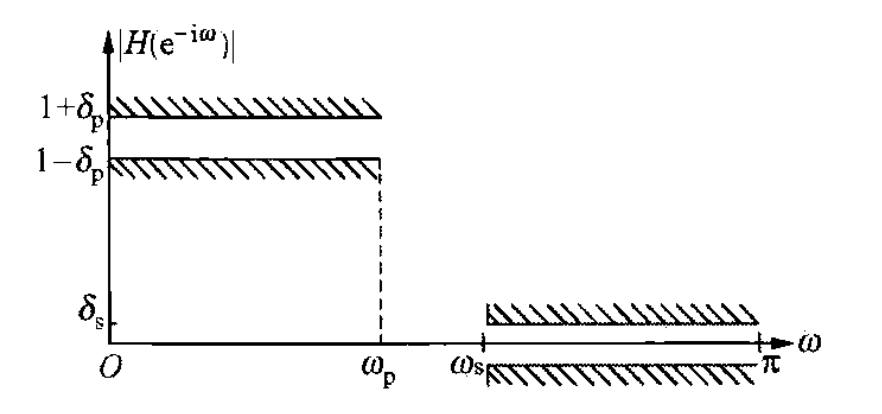
为设计Ⅰ类广义线性 FIR 滤波器,希望
A(e−iω)=k=0∑M/2a(k)coskω≈HL(e−iω)
系数 a(k) 需要使得频率域 F 上误差 E(e−iω) 的最大绝对值最小。
a(k)min(ω∈Fmax∣E(e−iω)∣),F=[0,ωp]∪[ωs,π]
该问题即切比雪夫最佳逼近问题,其数值解法为 Parks-McClellan 算法。