第四章：线性时不变滤波器与系统

约 1499 字大约 5 分钟

2026-01-29

注

本章核心：定义线性时不变系统及其基本性质；深入讨论系统的因果性、稳定性及组合方式（串联、并联、反馈）；重点阐述有理系统（递归滤波器）的Z变换表示与差分方程解法。

§1 线性时不变系统及其时间响应函数

1. 系统的一般定义

系统是一种将输入信号 $x(n)$ 映射为输出信号 $y(n)$ 的装置或数学模型。

y(n)=Tx(n)

2. 线性时不变系统

线性系统：满足叠加原理的系统。若输入 $x_1(t), x_2(t)$ 对应输出 $y_1(t), y_2(t)$ ，则输入 $ax_1(t) + bx_2(t)$ 对应输出 $ay_1(t) + by_2(t)$ 。
时不变系统：系统的特性不随时间变化。若输入 $x(t)$ 对应输出 $y(t)$ ，则输入 $x(t - t_0)$ 对应输出 $y(t - t_0)$ 。
注
时不变性质表明，输出信号的波形不随输入信号的延迟而改变，并且输出信号的延迟与输入信号的延迟是同步的。

3. 线性时不变系统的时间响应函数

当输入为单位冲激函数 $\delta(t)$ 时，系统的输出称为该系统的时间响应函数，记作 $h(t)$ 。

h(n) = T \delta(n)

相应地，线性时不变系统 $T$ 的频率响应函数和 Z 变换为

H(\omega)=\sum_{n=-\infty}^{+\infty}h(n)e^{-in\omega}

H(Z)=\sum_{n=-\infty}^{+\infty}h(n)Z^{n}

4. 线性时不变系统的输出信号

输出信号 $y(n)$ 与输入信号 $x(n)$ 和时间响应函数 $h(n)$ 的关系为：

y(n)=x(n)*h(n)

H(Z)=\frac{Y(Z)}{X(Z)}

§2 线性时不变系统的因果性和稳定性

1. 因果性

连续系统：若系统的时间响应函数 $h(t)$ 满足 $h(t) = 0$ 当 $t < 0$ ，则称该系统为因果系统或物理可实现系统。
离散系统：若系统的时间响应函数 $h(n)$ 满足 $h(n) = 0$ 当 $n < 0$ ，则称该系统为因果系统或物理可实现系统。

2. 稳定性

有界输入有界输出（BIBO）稳定性：若系统对任何有界输入信号 $x(n)$ （即存在常数 $C$ 使得 $|x(n)| \le C$ ）产生有界输出信号 $y(n)$ ，则称该系统具有有界输入有界输出稳定性。

定理 1

线性时不变系统 $h(n)$ 具有 BIBO 稳定性的充分必要条件是：

\sum_{n=-\infty}^{\infty} |h(n)| < +\infty

能量有限稳定性：若系统对任何能量有限的输入信号 $x(n)$ （即 $\sum_{n=-\infty}^{+\infty}x^2(n) < +\infty$ ）产生能量有限输出信号 $y(n)$ ，则称该系统具有能量有限稳定性。

定理 2

线性时不变系统 $h(n)$ 具有能量有限稳定性的充分必要条件是：存在一个正数 $C$ 使得

|H(\omega)|=\bigg|\sum_{n=-\infty}^{+\infty}h(n)e^{-in\omega}\bigg|\le C

§3 系统的组合：串联、并联及反馈

1. 串联组合

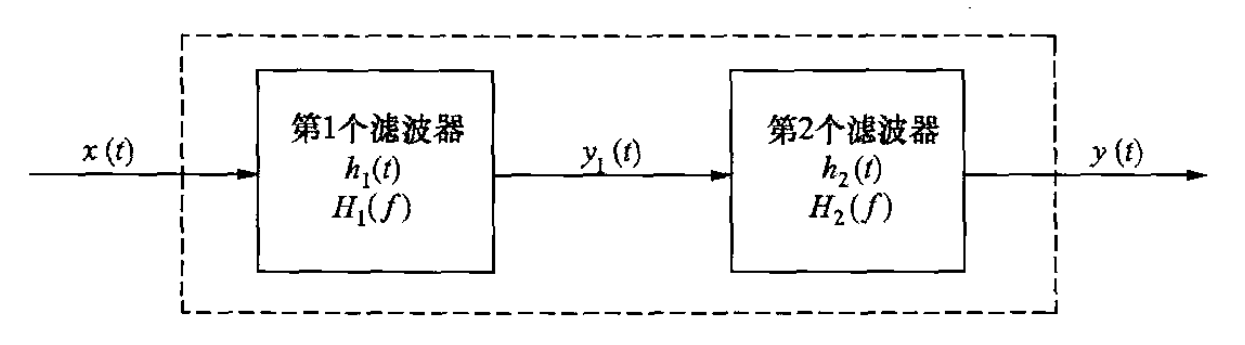
定义：两个系统 $T_1$ 和 $T_2$ 串联，指第一个系统的输出作为第二个系统的输入。

时间响应函数：若 $T_1$ 的时间响应函数为 $h_1(n)$ ， $T_2$ 的时间响应函数为 $h_2(n)$ ，则串联后系统的总时间响应函数为：

h(n) = h_1(n) * h_2(n)

Z 变换关系：若 $H_1(Z), H_2(Z)$ 分别为 $T_1, T_2$ 的 Z 变换，则总系统 Z 变换为：

H(Z) = H_1(Z) \cdot H_2(Z)

2. 并联组合

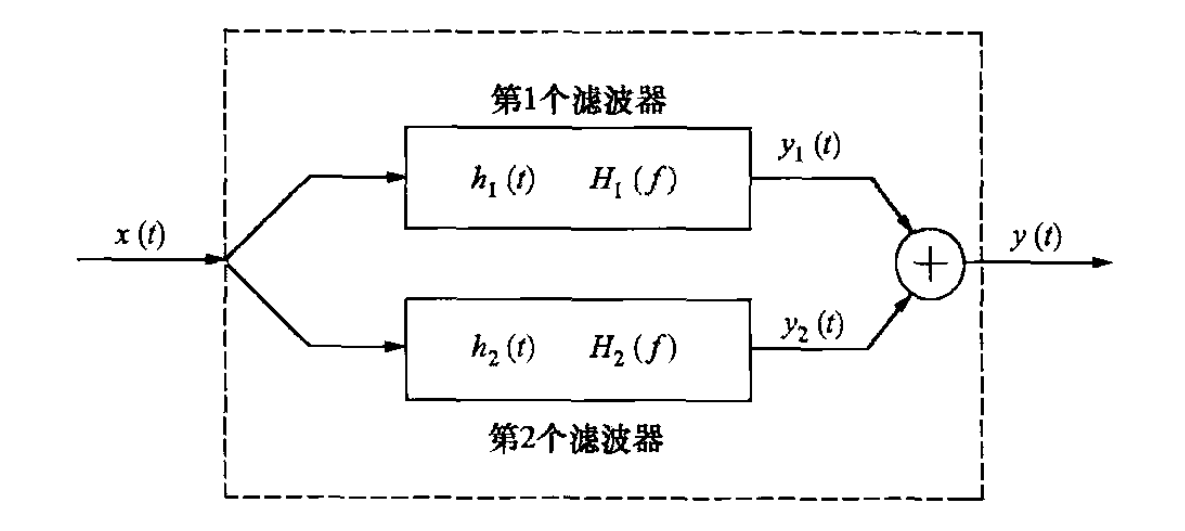
定义：两个系统 $T_1$ 和 $T_2$ 并联，指它们共享同一个输入，输出相加。

时间响应函数：若 $T_1$ 的时间响应函数为 $h_1(n)$ ， $T_2$ 的时间响应函数为 $h_2(n)$ ，则并联后系统的总时间响应函数为：

h(n) = h_1(n) + h_2(n)

Z 变换关系：若 $H_1(Z), H_2(Z)$ 分别为 $T_1, T_2$ 的 Z 变换，则总系统 Z 变换为：

H(Z) = H_1(Z) + H_2(Z)

3. 反馈组合

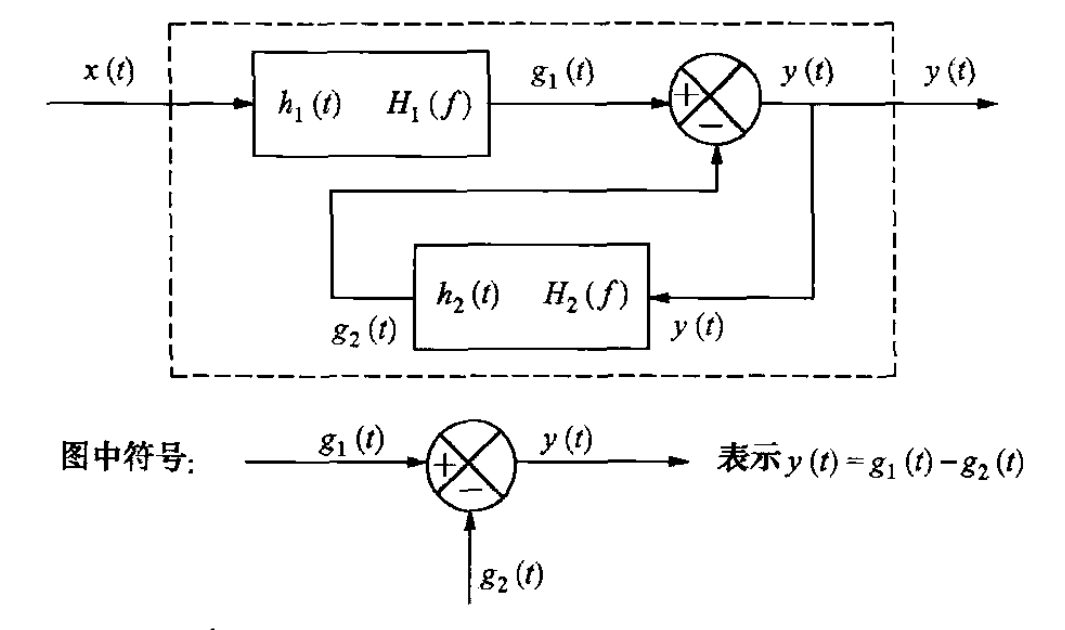
定义：系统的输出经过一个子系统后，再加入到输出中去。

时间域关系式

y(t) = x(t) * h_1(t) - y(t) * h_2(t)

Z 变换关系

Y(Z) = X(Z) H_1(Z) - Y(Z) H_2(Z)

H(Z) = \frac{Y(Z)}{X(Z)} = \frac{H_1(Z)}{1 + H_1(Z) H_2(Z)}

§4 有理系统及其时间响应函数

1. 有理系统

时间响应函数的 Z 变换 $H(Z)$ 为有理函数的系统称为有理系统。

H(Z) = \frac{B(Z)}{A(Z)}, \quad B(Z) = b_0 + b_1 Z + \cdots + b_q Z^q, \quad A(Z) = 1 + a_1 Z + \cdots + a_p Z^p

有理系统也称为递归系统或递归滤波器，因为其输出依赖于过去的输出值。

y(n) = \sum_{i=0}^{q} b_i x(n-i) - \sum_{j=1}^{p} a_j y(n-j)

2. 稳定有理系统的时间响应函数

稳定性条件：有理系统稳定的充分必要条件是其分母多项式 $A(Z)$ 在单位圆内及上无根，即所有极点位于单位圆外。

有理分式 $H(Z)$ 可分解为

H(Z)=\sum_{l=1}^{q-p}d_lZ^l+\sum_{j=1}^m\sum_{l_j=1}^{r_j}\frac{c_j(l_j)}{(Z-\alpha_j)^{l_j}}

其中 $\alpha_j$ 为分母 $A(Z)=1 + a_1 Z + \cdots + a_p Z^p$ 的 $r_j$ 重根， $\sum_{j=1}^mr_j=p$ 。

之后基于 $H(Z)$ 在单位圆内解析区域的罗朗展开，提取相应系数即得 $h(n)$ 。

§5 差分方程的单边 Z 变换解法

1. 单边 Z 变换

对因果序列 $x(n)$ （即 $x(n)=0$ 当 $n<0$ ），其单边 Z 变换定义为：

X(Z) = \sum_{n=0}^{\infty} x(n) Z^{n}

2. 解法步骤

写出差分方程：
$y(n) = \sum_{i=0}^{q} b_i x(n-i) - \sum_{j=1}^{p} a_j y(n-j)$
取单边 Z 变换：
$Y(Z) = \sum_{i=0}^{q} b_i Z^{i} X(Z) - \sum_{j=1}^{p} a_j Z^{j} Y(Z)$
解出 $Y(Z)$ ：
$Y(Z) = \frac{B(Z) X(Z)}{A(Z)}$
逆 Z 变换：通过部分分式展开或查表，得到时间响应函数 $y(n)$ 。

版权所有

版权归属：Staaaaaaaaar

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)