Sam's Blog

简体中文

English

简体中文

English

外观

第十一章：递归滤波器的设计

约 2497 字大约 8 分钟

2026-01-29

注

本章核心：介绍递归滤波器（IIR）的基本概念、稳定性判定；详述模拟滤波器设计原理（巴特沃斯、切比雪夫）；重点讲解双线性变换法将模拟滤波器转换为数字递归滤波器的过程；补充脉冲响应不变法及最优化设计思想。

§1 递归滤波及其稳定性

1. 递归滤波的基本形式

设输入信号为 x(t)x(t)，输出信号为 y(t)y(t)，递归滤波器的差分方程为：

y(t)=∑i=0nbix(t−i)−∑j=1majy(t−j)y(t) = \sum_{i=0}^{n} b_i x(t-i) - \sum_{j=1}^{m} a_j y(t-j)

其 Z 变换关系为：

Y(Z)=H(Z)X(Z),H(Z)=B(Z)A(Z),B(Z)=∑i=0nbiZi,A(Z)=1+∑j=1majZjY(Z) = H(Z) X(Z), \quad H(Z) = \frac{B(Z)}{A(Z)}, \quad B(Z) = \sum_{i=0}^{n} b_i Z^{i}, \quad A(Z) = 1 + \sum_{j=1}^{m} a_j Z^{j}

称 H(Z)H(Z) 为递归滤波器的系统函数或传递函数。

2. 递归滤波的稳定性

定义

若 y(t)y(t) 的初始值有误差

y~(t)=y(t)+ε(t),0≤t≤m−1\tilde{y}(t) = y(t) + \varepsilon(t),\quad 0 \leq t \leq m-1

令 e(t)=y~(t)−y(t)e(t) = \tilde{y}(t) - y(t)，由递推关系得

{e(t)=−∑j=1maje(t−j)t≥me(t)=ε(t)0≤t≤m−1\begin{cases} e(t) = -\sum_{j=1}^{m}a_j e(t-j) & t \geq m \\ e(t) = \varepsilon(t) & 0 \leq t \leq m-1 \end{cases}

若对任何初始噪声 ε(t)\varepsilon(t)，当 t→∞t \to \infty 时，有 e(t)→0e(t) \to 0，则称递归滤波是稳定的。

性质 1（稳定性定理）

递归滤波器稳定的充分必要条件是：多项式 A(Z)=1+a1Z+⋯+amZmA(Z) = 1 + a_1 Z + \cdots + a_m Z^m 的根全部在单位圆外。

提示

此性质等价于第四章 §2 中关于线性时不变系统稳定性的结论。

3. 正向与反向递归滤波

  • 正向递归滤波：从 t=mt = m 开始，利用初始值 y(0),y(1),…,y(m−1)y(0), y(1), \dots, y(m-1) 向后递推计算 y(t)y(t)。
  • 反向递归滤波：从 t=−mt = -m 开始，利用初始值 y(−m+1),…,y(0)y(-m+1), \dots, y(0) 向前递推计算 y(t)y(t)。

y(t)=∑i=0nbix(t+i)−∑j=1majy(t+j)y(t) = \sum_{i=0}^{n} b_i x(t+i) - \sum_{j=1}^{m} a_j y(t+j)

性质 2（反向递归滤波稳定性）

反向递归滤波器稳定的充分必要条件是：多项式 A(Z)A(Z) 的根全部在单位圆外。

注

当滤波器分母多项式根在单位圆内时，应采用反向递归滤波。

§2 模拟滤波器的设计

在无线电工程中，已设计出许多电滤波器（由电阻、电容等元件组成），可对连续信号进行低通、高通、带通、带阻等滤波。这类处理连续信号的电滤波器称为模拟滤波器。其脉冲响应为 h(t)h(t)，频率响应为：

H(ω)=∫−∞∞h(t)e−iωtdtH(\omega) = \int_{-\infty}^{\infty} h(t) e^{-i\omega t} dt

本节讨论如何根据技术指标设计不同类型的模拟滤波器，主要包括巴特沃斯滤波器和切比雪夫滤波器。

1. 低通模拟滤波器的设计

由于模拟滤波器无法达到理想滤波器的效果，只能提出近似的要求。

假定 ωc=1\omega_c=1 ，可以设低通模拟滤波器的振幅谱平方为：

∣H(ω)∣2=11+g2(ω)|H(\omega)|^2 = \frac{1}{1 + g^2(\omega)}

其中 g(ω)g(\omega) 是 ω\omega 的实系数有理函数，且满足：

  • ∣g(−ω)∣=∣g(ω)∣|g(-\omega)| = |g(\omega)|
  • 当 ω<1\omega < 1 时，g(ω)≈0g(\omega) \approx 0（通带内波动小）
  • 当 ω>1\omega > 1 时，g(ω)≈∞g(\omega) \approx \infty（阻带内衰减大）

由于 ∣H(ω)∣2|H(\omega)|^2 是 ω\omega 的有理函数，可表示为：

∣H(ω)∣2=P1(ω)P2(ω)|H(\omega)|^2 = \frac{P_1(\omega)}{P_2(\omega)}

其中 P1(ω),P2(ω)P_1(\omega), P_2(\omega) 为实系数多项式，且当 ω\omega 取实值时，P1(ω)>0,P2(ω)>0P_1(\omega) > 0, P_2(\omega) > 0。

设 αj\alpha_j 为 P1(ω)P_1(\omega) 的虚部大于0的根，βi\beta_i 为 P2(ω)P_2(\omega) 的虚部大于0的根，则

∣H(ω)∣2=k2(ω−α1)(ω−α‾1)(ω−α2)(ω−α‾2)⋯(ω−β1)(ω−β‾1)(ω−β2)(ω−β‾2)⋯|H(\omega)|^2 = k^2 \frac{(\omega - \alpha_1)(\omega - \overline{\alpha}_1)(\omega - \alpha_2)(\omega - \overline{\alpha}_2)\cdots}{(\omega - \beta_1)(\omega - \overline{\beta}_1)(\omega - \beta_2)(\omega - \overline{\beta}_2)\cdots}

取

H(ω)=k(ω−α1)(ω−α2)⋯(ω−β1)(ω−β2)⋯H(\omega) = k \frac{(\omega - \alpha_1)(\omega - \alpha_2)\cdots}{(\omega - \beta_1)(\omega - \beta_2)\cdots}

则 H(ω)H(\omega) 为在 ω\omega 的下半平面内无零点和极点，为最小相位滤波器，并可通过模拟电路实现。

注

巴特沃斯低通滤波器：g(ω)=ωng(\omega)=\omega^n

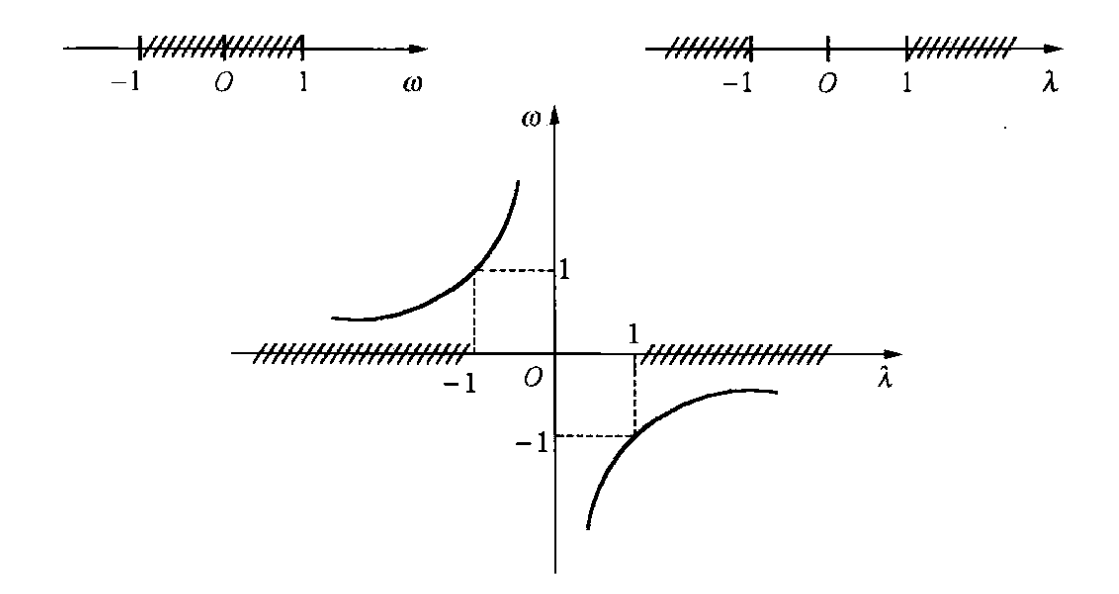
切比雪夫低通滤波器：g(ω)=εTn(ω)=εcos⁡(narccos⁡ω)g(\omega)=\varepsilon T_n(\omega)=\varepsilon\cos (n\arccos\omega)

2. 高通模拟滤波器的设计

通过频率变换将低通滤波器转换为高通滤波器：

ω=−1λ\omega = -\frac{1}{\lambda}

代入低通滤波器频谱 H(ω)H(\omega)，得到高通滤波器频谱 H(λ)H(\lambda)。

3. 带通模拟滤波器的设计

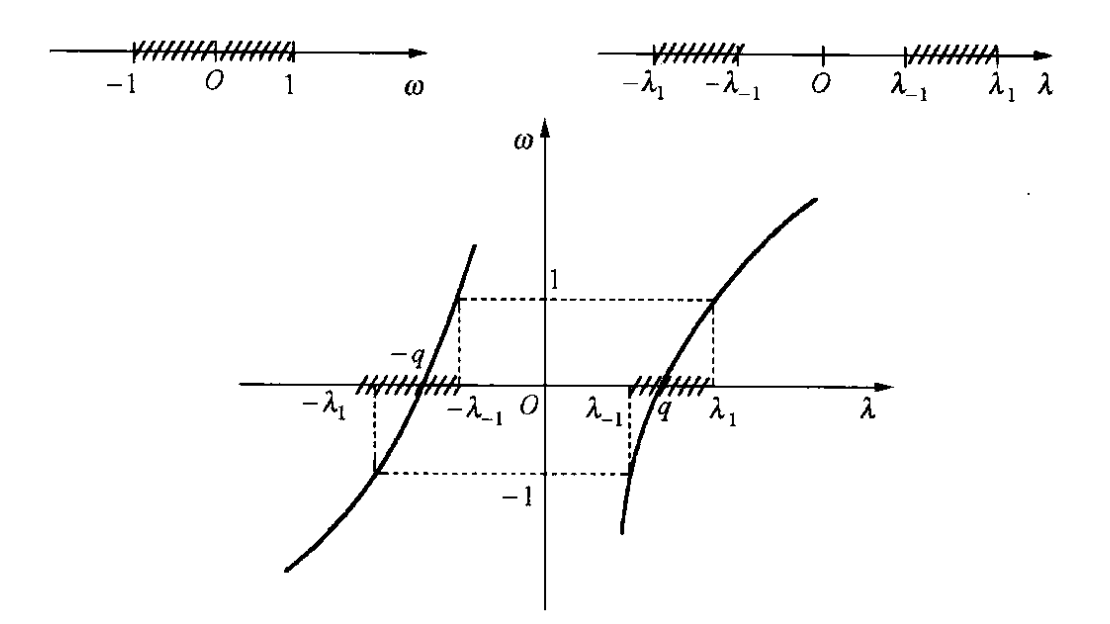
通过频率变换：

ω=λ−q2λq>0\omega = \lambda - \frac{q^2}{\lambda}\quad q>0

代入低通滤波器频谱 H(ω)H(\omega)，得到高通滤波器频谱 H(λ)H(\lambda)。该变换将低通区间 [−1,1][-1, 1] 映射为带通区间 [−λ1,−λ−1]∪[λ−1,λ1][-\lambda_1, -\lambda_{-1}] \cup [\lambda_{-1}, \lambda_1]。

4. 带阻模拟滤波器的设计

通过组合高通和带通变换：

ω=−1λ−q2λ=1q2λ−λq>0\omega = -\frac{1}{\lambda-\frac{q^2}{\lambda}}= \frac{1}{\frac{q^2}{\lambda}-\lambda}\quad q>0

该变换将低通区间 [−1,1][-1, 1] 映射为带阻区间 [−λ1,−λ−1]∪[λ−1,λ1][-\lambda_1, -\lambda_{-1}] \cup [\lambda_{-1}, \lambda_1]。

5. 巴特沃斯低通模拟滤波器

注

∣H(ω)∣2=11+ω2n|H(\omega)|^2 = \frac{1}{1 + \omega^{2n}}

∣H(0)∣=1∣H(ω0)∣=12|H(0)|=1 \quad |H(\omega_0)|=\frac{1}{\sqrt{2}}

20lg⁡∣H(0)∣H(ωc)∣=10lg⁡2=3.0103dB 20\lg\frac{|H(0)}{|H(\omega_c)|}=10\lg2=3.0103 \text{dB}

因此称 ωc\omega_c 为 3dB 截止频率，当 ωc=1\omega_c=1 时，巴特沃斯低通滤波器称为归一化巴特沃斯低通模拟滤波器。

极点分布

极点 βk\beta_k 满足：

βk2n=−1=ei(2k−1)π,k=1,2,…,2n\beta_k^{2n} = -1 = e^{i(2k-1)\pi}, \quad k=1,2,\dots,2n

解得：

βk=ei(2k−1)π/(2n),k=1,2,…,2n\beta_k = e^{i(2k-1)\pi/(2n)}, \quad k=1,2,\dots,2n

在上半平面的极点为 βk,k=1,2,…,n\beta_k, k=1,2,\dots,n。

一般形式

H(ω)=1(ω−β1)(ω−β2)⋯(ω−βn)H(\omega) = \frac{1}{(\omega - \beta_1)(\omega - \beta_2)\cdots(\omega - \beta_n)}

其中 βk=ei(2k−1)π/(2n)\beta_k = e^{i(2k-1)\pi/(2n)}。

具体实例

  • 一阶巴特沃斯：

    H(ω)=1ω−iH(\omega) = \frac{1}{\omega - i}

  • 二阶巴特沃斯：

    H(ω)=1ω2−i2ω−1H(\omega) = \frac{1}{\omega^2 - i\sqrt{2}\omega - 1}

  • 三阶巴特沃斯：

    H(ω)=1(ω−i)(ω−iω−1)H(\omega) = \frac{1}{(\omega - i)(\omega - i\omega - 1)}

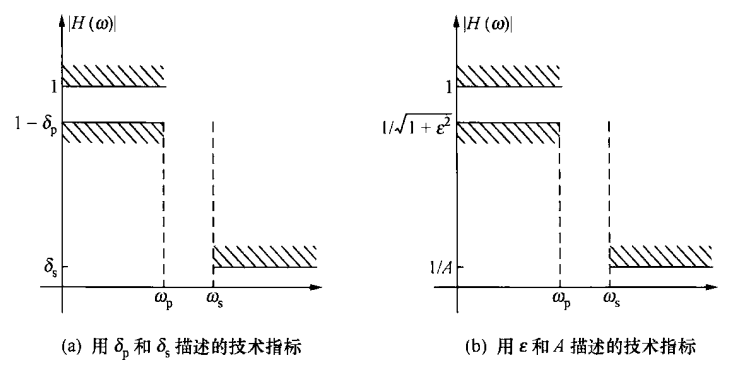
6. 低通模拟滤波的技术要求

给定技术要求：通带截止频率 fpf_p，阻带截止频率 fsf_s，通带波动 δp\delta_p，阻带波动 δs\delta_s。

A=1δsδp=1−11+ε2A=\frac{1}{\delta_s}\quad \delta_p=1-\frac{1}{\sqrt{1+\varepsilon^2}}

需要设计一个巴特沃斯低通模拟滤波器。

  1. 计算判别因子 dd 和选择性因子 kk：

    d=((1−δp)−2−1δs−2−1)1/2=εA2−1,k=ωpωsd = \left(\frac{(1-\delta_p)^{-2}-1}{\delta_s^{-2} - 1}\right)^{1/2}=\frac{\varepsilon}{\sqrt{A^2-1}}, \quad k = \frac{\omega_p}{\omega_s}

  2. 确定阶数 nn：

    n≥lg⁡dlg⁡kn \ge \frac{\lg d}{\lg k}

  3. 确定 3dB 截止频率 ωc\omega_c：

    ωp((1−δp)−2−1)−1/2n≤ωc≤ωs(δs−2−1)−1/2n\omega_p((1-\delta_p)^{-2}-1)^{-1/2n} \leq \omega_c \leq \omega_s(\delta_s^{-2}-1)^{-1/2n}

  4. 由 nn 和 ωc\omega_c 确定巴特沃斯滤波器。

§3 数字递归滤波器的设计

1. 双线性变换

双线性变换定义为

ω=Ai⋅1−Z1+Z,A>0\omega=\frac{A}{i}\cdot\frac{1-Z}{1+Z},\quad A>0 \\

当 ZZ 在单位圆上取值时，有

Z=e−iφ,φ=2πΔfZ=e^{-i\varphi},\quad \varphi=2\pi \Delta f

ω=Atan⁡φ2\omega = A\tan\frac{\varphi}{2}

这表明，双线性变换把 ZZ 平面的单位圆变成了 ω\omega 平面的实轴。ω\omega 平面的下半平面与 ZZ 平面的单位圆内相对应，ω\omega 平面的上半平面与 ZZ 平面的单位圆外相对应。

2. 数字递归滤波器

低通数字递归滤波器

设低通范围为 [−f1,f1][-f_1, f_1]，对应的 ZZ 平面点为 Z=e±i2πf1Δ=e±iφ1Z = e^{\pm i 2\pi f_1 \Delta}= e^{\pm i \varphi_1}。通过对应关系可得双线性变换

Z 平面的 e−iφ1↔ω 平面的 1Z\text{ 平面的 }e^{-i\varphi_1}\leftrightarrow \omega \text{ 平面的 } 1

ω=1itan⁡πΔf1⋅1−Z1+Z\omega=\frac{1}{i\tan\pi\Delta f_1}\cdot\frac{1-Z}{1+Z}

注

以一阶巴特沃斯低通模拟滤波器为例：

H(Z)=1+Z(1+A)+(1−A)Z,A=1tan⁡(πΔf1)H(Z) = \frac{1 + Z}{(1 + A) + (1 - A)Z}, \quad A = \frac{1}{\tan(\pi \Delta f_1)}

带通数字递归滤波器

设带通范围为 [−f2,−f1]∪[f1,f2][-f_2, -f_1] \cup [f_1, f_2]，令

φ1=2πΔf1φ2=2πΔf2\varphi_1=2\pi\Delta f_1\quad\varphi_2=2\pi\Delta f_2

由前带通模拟滤波器的设计，此时应考虑 λ\lambda 平面与 ZZ 平面的双线性变换

λ=Ai⋅1−Z1+Z,A>0\lambda=\frac{A}{i}\cdot\frac{1-Z}{1+Z},\quad A>0

Z 平面的 e−iφ1↔λ 平面的 λ−1Z \text{ 平面的 }e^{-i\varphi_1}\leftrightarrow \lambda \text{ 平面的 } \lambda_{-1}

Z 平面的 e−iφ2↔λ 平面的 λ1Z \text{ 平面的 }e^{-i\varphi_2}\leftrightarrow \lambda \text{ 平面的 } \lambda_{1}

结合对应关系和带通模拟滤波器的映射关系，有下面关系式

A=1tan⁡φ22−tan⁡φ12=1tan⁡πΔf2−tan⁡πΔf1A = \frac{1}{\tan \frac{\varphi_2}{2} - \tan \frac{\varphi_1}{2}} = \frac{1}{\tan \pi \Delta f_2 - \tan \pi \Delta f_1}

q2=A2tan⁡φ12tan⁡φ22=A2tan⁡πΔf1tan⁡πΔf2q^2 = A^2 \tan \frac{\varphi_1}{2} \tan \frac{\varphi_2}{2} = A^2 \tan \pi \Delta f_1 \tan \pi \Delta f_2

最终的变换关系为

ω=λ−q2λ=−iA1−Z1+Z+q2iA1−Z1+Z=(A2+q2)+2(q2−A2)Z+(A2+q2)Z2iA(1−Z2)=1+2μZ+Z2iν(1−Z2)\begin{aligned} \omega &= \lambda - \frac{q^2}{\lambda} = -\mathrm{i}A \frac{1 - Z}{1 + Z} + \frac{q^2}{\mathrm{i}A \frac{1 - Z}{1 + Z}} \\\\ &= \frac{(A^2 + q^2) + 2(q^2 - A^2)Z + (A^2 + q^2)Z^2}{\mathrm{i}A(1 - Z^2)} \\\\ &= \frac{1 + 2\mu Z + Z^2}{\mathrm{i}\nu(1 - Z^2)} \end{aligned}

其中

μ=q2−A2A2+q2=−cos⁡πΔ(f1+f2)cos⁡πΔ(f2−f1)\mu = \frac{q^2 - A^2}{A^2 + q^2}=\frac{-\cos \pi \Delta (f_1 + f_2)}{\cos \pi \Delta (f_2 - f_1)}

ν=AA2+q2=tan⁡πΔ(f2−f1)\nu = \frac{A}{A^2 + q^2}=\tan \pi \Delta (f_2 - f_1)

注

以一阶巴特沃斯低通模拟滤波器为例：

H(Z)=ν(1−Z2)(1+ν)+2μZ+(1−ν)Z2H(Z) = \frac{\nu(1 - Z^2)}{(1 + \nu) + 2\mu Z + (1 - \nu)Z^2}

带阻数字递归滤波器

设带阻范围为 [−f2,−f1]∪[f1,f2][-f_2, -f_1] \cup [f_1, f_2]，参照带通数字递归滤波器的设计方法可得

ω=−iν(1−Z2)1+2μZ+Z2\omega = \frac{-\mathrm{i}\nu(1 - Z^2)}{1 + 2\mu Z + Z^2}

其中

μ=q2−A2A2+q2=−cos⁡πΔ(f1+f2)cos⁡πΔ(f2−f1)\mu = \frac{q^2 - A^2}{A^2 + q^2}=\frac{-\cos \pi \Delta (f_1 + f_2)}{\cos \pi \Delta (f_2 - f_1)}

ν=AA2+q2=tan⁡πΔ(f2−f1)\nu = \frac{A}{A^2 + q^2}=\tan \pi \Delta (f_2 - f_1)

注

以一阶巴特沃斯低通模拟滤波器为例：

H(Z)=1+2μZ+Z2(1+ν)+2μZ+(1−ν)Z2H(Z) = \frac{1 + 2\mu Z + Z^2}{(1 + \nu) + 2\mu Z + (1 - \nu)Z^2}

高通数字递归滤波器

设高通范围为 [−1/(2Δ),−f1]∪[f1,1/(2Δ)][-1/(2\Delta), -f_1] \cup [f_1, 1/(2\Delta)]，则对应变换为

ω=1iA⋅1+Z1−Z=−itan⁡πΔf1⋅1+Z1−Z\omega=\frac{1}{iA}\cdot\frac{1+Z}{1-Z}=-i\tan\pi\Delta f_1\cdot\frac{1+Z}{1-Z}

注

以一阶巴特沃斯低通模拟滤波器为例：

H(Z)=1−Z(tan⁡(πΔf1)+1)+(tan⁡(πΔf1)−1)ZH(Z) = \frac{1 - Z}{(\tan(\pi \Delta f_1) + 1) + (\tan(\pi \Delta f_1) - 1)Z}

3. 关于递归滤波器设计的说明

  • Z 平面法
  • 最优化法
  • 转换法
    • 频率域转换法：把模拟滤波器的频谱通过双线性变换转换为数字递归滤波器的 Z 变换
    • 时间域转换法——脉冲响应不变转换法：把模拟滤波器脉冲响应 h(t)h(t)，以 Δ\Delta 为抽样间隔直接抽样得 h(nΔ)h(n\Delta)，由此可得数字递归滤波器 ZZ 变换 H(Z)=∑n=0+∞h(nΔ)ZnH(Z) = \sum_{n=0}^{+\infty} h(n\Delta) Z^n。

版权归属：Staaaaaaaaar

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)