ICS - Cache Lab | “百发百中”的缓存
在 Cache Lab 中,我们将使用缓存的基本概念和工作原理,编写缓存模拟器并优化矩阵转置程序。实验分为两个部分:
- Part A:编写一个 C 程序,用于模拟硬件缓存内存的行为。
- Part B:优化一个矩阵转置函数,目标是尽量减少缓存未命中的次数。
预备知识
缓存概念
CPU 与主存间的高速缓冲存储器,容量小、速度快,用于暂存主存中高频访问的数据,缓解 CPU 与主存的速度鸿沟,核心依托局部性原理工作。
缓存原理
缓存通过“映射-查找-替换-写回”实现数据管理:主存数据按块映射到缓存;CPU 访问时先查缓存,命中则直接读取,未命中则调主存块;缓存满时按策略(如 LRU)替换旧块;写操作分写直达(同步写主存)和写回(替换时写主存)等策略。
前置准备
内存映射可视化
由于缓存的工作原理较为抽象,建议使用可视化工具(可编写脚本实现)来帮助理解缓存的映射、命中和替换过程。通过图形化界面,可以直观地观察不同访问模式下缓存的行为,有助于后续实验的设计与调试。
Part A
在 Part A 中,我们需要编写一个缓存模拟器 csim.c,以 valgrind 内存追踪文件作为输出,模拟缓存在内存跟踪上的行为,并输出命中次数、未命中次数和驱逐次数的总数。驱逐策略使用 LRU 策略。模拟器程序需要接受以下命令行参数:
Usage: ./csim [-hv] -s <num> -E <num> -b <num> -t <file>
-h Print this help message.
-v Optional verbose flag.
-s <num> Number of set index bits.
-E <num> Number of lines per set.
-b <num> Number of block offset bits.
-t <file> Trace file.valgrind 内存追踪文件内容如下:
I 0400d7d4,8
M 0421c7f0,4
L 04f6b868,8
S 7ff0005c8,8每行的格式是:
[space]operation address,size操作字段表示内存访问的类型:
I表示指令加载L表示数据加载S表示数据存储M表示数据修改(即先加载数据然后存储数据)
每个 I 之前不留空格;在每个 M、L 和 S 之前总是留有空格。地址字段指定一个 64 位的十六进制内存地址。大小字段指定操作访问的字节数。
此外,程序还需要提供 verbose 选项。verbose 模式下,需要输出每条内存追踪信息的缓存行为。例如:
./csim -s 4 -E 1 -b 4 -t traces/yi.trace
hits:4 misses:5 evictions:3./csim -v -s 4 -E 1 -b 4 -t traces/yi.trace
L 10,1 miss
M 20,1 miss hit
L 22,1 hit
S 18,1 hit
L 110,1 miss eviction
L 210,1 miss eviction
M 12,1 miss eviction hit
hits:4 misses:5 evictions:3解析命令行参数
为了能够读取输入信息,我们首先需要进行命令行参数解析,推荐使用 getopt 来解析,它能自动处理选项与参数的匹配。
参考代码如下:
#include <getopt.h>
#include <stdlib.h>
#include <unistd.h>
int s = 0, E = 0, b = 0;
char *trace_file = NULL;
int verbose = 0;
void print_usage() {
printf("Usage: ./csim [-hv] -s <num> -E <num> -b <num> -t <file>\n");
printf("-h Print this help message.\n");
printf("-v Optional verbose flag.\n");
printf("-s <num> Number of set index bits.\n");
printf("-E <num> Number of lines per set.\n");
printf("-b <num> Number of block offset bits.\n");
printf("-t <file> Trace file.\n");
}
int opt;
while ((opt = getopt(argc, argv, "hvs:E:b:t:")) != -1) {
switch (opt) {
case 'h':
print_usage();
exit(0);
case 'v':
verbose = 1;
break;
case 's':
s = atoi(optarg);
break;
case 'E':
E = atoi(optarg);
break;
case 'b':
b = atoi(optarg);
break;
case 't':
trace_file = optarg;
break;
default:
print_usage();
exit(1);
}
}初始化缓存
由于我们的模拟器必须能够正确处理任意的 s、E 和 b。这意味着我们需要使用 malloc 函数为模拟器的数据结构分配存储空间。
我们定义缓存结构如下:
// Cache line structure
typedef struct {
int valid;
unsigned long long tag;
int lru_counter;
} cache_line;
// Cache set structure
typedef struct {
cache_line *lines;
} cache_set;
// Cache structure
typedef struct {
int s;
int E;
int b;
cache_set *sets;
} cache;在开始模拟前需要对缓存进行初始化:
// Function to initialize the cache
cache init_cache(int s, int E, int b) {
cache new_cache;
new_cache.s = s;
new_cache.E = E;
new_cache.b = b;
int S = 1 << s; // Number of sets
new_cache.sets = (cache_set *)malloc(S * sizeof(cache_set));
for (int i = 0; i < S; i++) {
new_cache.sets[i].lines = (cache_line *)malloc(E * sizeof(cache_line));
for (int j = 0; j < E; j++) {
new_cache.sets[i].lines[j].valid = 0;
new_cache.sets[i].lines[j].tag = 0;
new_cache.sets[i].lines[j].lru_counter = 0;
}
}
return new_cache;
}并在模拟结束后释放内存:
// Function to free the cache memory
void free_cache(cache my_cache) {
int S = 1 << my_cache.s;
for (int i = 0; i < S; i++) {
free(my_cache.sets[i].lines);
}
free(my_cache.sets);
}缓存行为实现
整个程序最核心的部分便是如何实现缓存行为,处理一条访存的主要流程为:
- 地址拆分:
set_index = (address >> b) & ((1ULL << s) - 1);tag = address >> (s + b);
- 定位目标集合:
cache_set *set = &cache->sets[set_index]; - LRU 更新:使用“最近最少使用”策略,对集合中所有有效行
lru_counter++。 - 命中检测:遍历行,若
valid && tag匹配:hit_count++;- 重置该行
lru_counter=0; - verbose 输出
hit;返回。
- 未命中处理:
miss_count++,verbose 输出miss。 - 查找空行:若存在
valid==0:填入tag,valid=1,lru_counter=0,返回。 - 驱逐处理:
eviction_count++,verbose 输出eviction;- 选择
lru_counter最大的行(最久未用)。 - 替换其
tag并将lru_counter=0。
参考代码如下:
// Function to simulate a memory access
void access_cache(cache *my_cache, unsigned long long address, int verbose) {
int s = my_cache->s;
int E = my_cache->E;
int b = my_cache->b;
unsigned long long set_index_mask = (1 << s) - 1;
unsigned long long set_index = (address >> b) & set_index_mask;
unsigned long long tag = address >> (s + b);
cache_set *current_set = &my_cache->sets[set_index];
// Update LRU counters for the set
for (int i = 0; i < E; i++) {
if (current_set->lines[i].valid) {
current_set->lines[i].lru_counter++;
}
}
// Check for hit
for (int i = 0; i < E; i++) {
if (current_set->lines[i].valid && current_set->lines[i].tag == tag) {
hit_count++;
if (verbose) printf(" hit");
current_set->lines[i].lru_counter = 0; // Reset LRU counter on hit
return;
}
}
// Miss
miss_count++;
if (verbose) printf(" miss");
// Find an empty line
for (int i = 0; i < E; i++) {
if (!current_set->lines[i].valid) {
current_set->lines[i].valid = 1;
current_set->lines[i].tag = tag;
current_set->lines[i].lru_counter = 0;
return;
}
}
// Eviction
eviction_count++;
if (verbose) printf(" eviction");
int max_lru = -1;
int evict_index = -1;
for (int i = 0; i < E; i++) {
if (current_set->lines[i].lru_counter > max_lru) {
max_lru = current_set->lines[i].lru_counter;
evict_index = i;
}
}
current_set->lines[evict_index].tag = tag;
current_set->lines[evict_index].lru_counter = 0;
}整合所有部分,再添加必要的内存追踪文件的读取和解析部分,最终完整 csim.c 代码呈现如下:
#include "cachelab.h"
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <unistd.h>
#include <getopt.h>
// Cache line structure
typedef struct {
int valid;
unsigned long long tag;
int lru_counter;
} cache_line;
// Cache set structure
typedef struct {
cache_line *lines;
} cache_set;
// Cache structure
typedef struct {
int s;
int E;
int b;
cache_set *sets;
} cache;
// Global variables for results
int hit_count = 0;
int miss_count = 0;
int eviction_count = 0;
// Function to initialize the cache
cache init_cache(int s, int E, int b) {
cache new_cache;
new_cache.s = s;
new_cache.E = E;
new_cache.b = b;
int S = 1 << s; // Number of sets
new_cache.sets = (cache_set *)malloc(S * sizeof(cache_set));
for (int i = 0; i < S; i++) {
new_cache.sets[i].lines = (cache_line *)malloc(E * sizeof(cache_line));
for (int j = 0; j < E; j++) {
new_cache.sets[i].lines[j].valid = 0;
new_cache.sets[i].lines[j].tag = 0;
new_cache.sets[i].lines[j].lru_counter = 0;
}
}
return new_cache;
}
// Function to free the cache memory
void free_cache(cache my_cache) {
int S = 1 << my_cache.s;
for (int i = 0; i < S; i++) {
free(my_cache.sets[i].lines);
}
free(my_cache.sets);
}
// Function to simulate a memory access
void access_cache(cache *my_cache, unsigned long long address, int verbose) {
int s = my_cache->s;
int E = my_cache->E;
int b = my_cache->b;
unsigned long long set_index_mask = (1 << s) - 1;
unsigned long long set_index = (address >> b) & set_index_mask;
unsigned long long tag = address >> (s + b);
cache_set *current_set = &my_cache->sets[set_index];
// Update LRU counters for the set
for (int i = 0; i < E; i++) {
if (current_set->lines[i].valid) {
current_set->lines[i].lru_counter++;
}
}
// Check for hit
for (int i = 0; i < E; i++) {
if (current_set->lines[i].valid && current_set->lines[i].tag == tag) {
hit_count++;
if (verbose) printf(" hit");
current_set->lines[i].lru_counter = 0; // Reset LRU counter on hit
return;
}
}
// Miss
miss_count++;
if (verbose) printf(" miss");
// Find an empty line
for (int i = 0; i < E; i++) {
if (!current_set->lines[i].valid) {
current_set->lines[i].valid = 1;
current_set->lines[i].tag = tag;
current_set->lines[i].lru_counter = 0;
return;
}
}
// Eviction
eviction_count++;
if (verbose) printf(" eviction");
int max_lru = -1;
int evict_index = -1;
for (int i = 0; i < E; i++) {
if (current_set->lines[i].lru_counter > max_lru) {
max_lru = current_set->lines[i].lru_counter;
evict_index = i;
}
}
current_set->lines[evict_index].tag = tag;
current_set->lines[evict_index].lru_counter = 0;
}
void print_usage() {
printf("Usage: ./csim [-hv] -s <num> -E <num> -b <num> -t <file>\n");
printf("-h Print this help message.\n");
printf("-v Optional verbose flag.\n");
printf("-s <num> Number of set index bits.\n");
printf("-E <num> Number of lines per set.\n");
printf("-b <num> Number of block offset bits.\n");
printf("-t <file> Trace file.\n");
}
int main(int argc, char *argv[]) {
int s = 0, E = 0, b = 0;
char *trace_file = NULL;
int verbose = 0;
int opt;
while ((opt = getopt(argc, argv, "hvs:E:b:t:")) != -1) {
switch (opt) {
case 'h':
print_usage();
exit(0);
case 'v':
verbose = 1;
break;
case 's':
s = atoi(optarg);
break;
case 'E':
E = atoi(optarg);
break;
case 'b':
b = atoi(optarg);
break;
case 't':
trace_file = optarg;
break;
default:
print_usage();
exit(1);
}
}
if (s == 0 || E == 0 || b == 0 || trace_file == NULL) {
printf("Error: Missing required command-line argument\n");
print_usage();
exit(1);
}
cache my_cache = init_cache(s, E, b);
FILE *file = fopen(trace_file, "r");
if (file == NULL) {
printf("Error: Cannot open trace file %s\n", trace_file);
exit(1);
}
char operation;
unsigned long long address;
int size;
char line[256];
while (fgets(line, sizeof(line), file)) {
if (line[0] == 'I') {
continue;
}
// sscanf returns the number of items successfully read
if (sscanf(line, " %c %llx,%d", &operation, &address, &size) == 3) {
if (verbose) {
printf("%c %llx,%d", operation, address, size);
}
switch (operation) {
case 'L':
access_cache(&my_cache, address, verbose);
break;
case 'S':
access_cache(&my_cache, address, verbose);
break;
case 'M':
access_cache(&my_cache, address, verbose); // Load
access_cache(&my_cache, address, verbose); // Store
break;
}
if (verbose) {
printf("\n");
}
}
}
fclose(file);
free_cache(my_cache);
printSummary(hit_count, miss_count, eviction_count);
return 0;
}编译并测试:
make && ./test-csim Your simulator Reference simulator
Points (s,E,b) Hits Misses Evicts Hits Misses Evicts
3 (1,1,1) 11 8 6 11 8 6 traces/yi2.trace
3 (4,2,4) 4 5 2 4 5 2 traces/yi.trace
3 (2,1,4) 2 3 1 2 3 1 traces/dave.trace
3 (2,1,3) 694 453 449 694 453 449 traces/mem.trace
3 (2,2,3) 201 37 29 201 37 29 traces/trans.trace
3 (2,4,3) 212 26 10 212 26 10 traces/trans.trace
3 (5,1,5) 231 7 0 231 7 0 traces/trans.trace
6 (5,1,5) 265189 21777 21745 265189 21777 21745 traces/long.trace
27
TEST_CSIM_RESULTS=27Part B
在 Part B 中,我们需要在 trans.c 中编写一个矩阵转置函数,使缓存未命中次数在规定范围内。缓存类型为直接映射缓存,缓存容量固定为 1KB,块大小为 32 字节。
void trans(int M, int N, int A[N][M], int B[M][N]);具体而言,函数接受四个参数,计算 N × M 矩阵 A 的转置,并将结果存储在 M × N 矩阵 B 中。
我们将处理三种不同大小的矩阵,并针对这三种情况进行优化。这也意味着,我们可以明确检查输入大小,并为每种情况实现单独优化的代码。
32 × 32
32 × 32 矩阵的转置要求 miss 数量控制在 300 以内。首先观察一下矩阵的缓存映射结构。
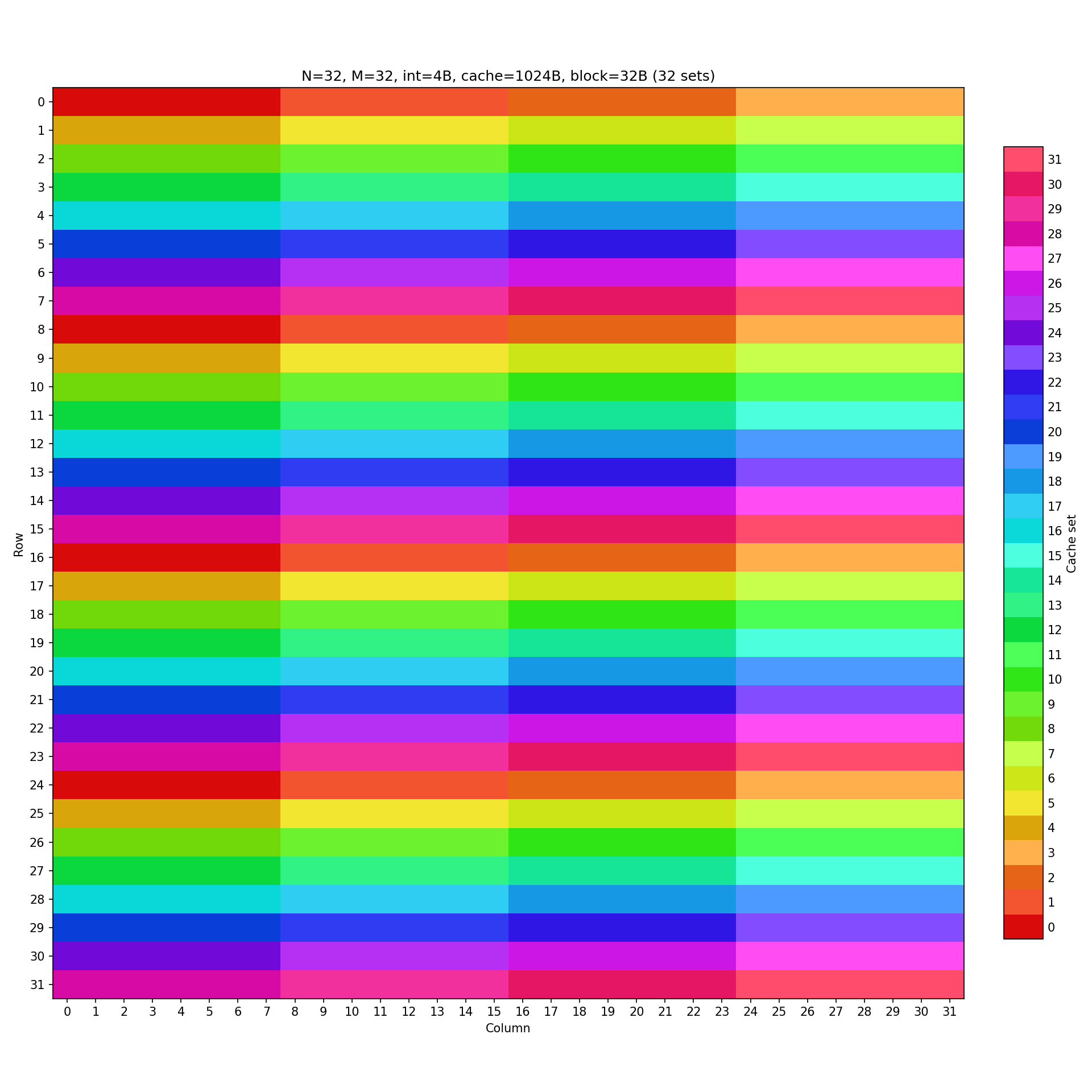
如果我们直接采用最朴素的方法,按行列依次将 A 矩阵的元素转移到 B 矩阵对应位置上。
void trans_32_32(int M, int N, int A[N][M], int B[M][N])
{
int i, j, tmp;
for (i = 0; i < N; i++) {
for (j = 0; j < M; j++) {
tmp = A[i][j];
B[j][i] = tmp;
}
}
}简单估计一下这个函数产生的 miss 数量:
- A 矩阵行优先访问,可以充分利用整个块,仅在每次装载一个新块时产生 miss,概率为 1/8。
- B 矩阵列优先访问,由于矩阵大小不足以填充整个缓存,因此每次对 B 矩阵元素的访问都会产生一次 miss,概率为 1。
综合考虑最终 miss 数量大致为 (32 × 32) × (1/8 + 1) = 1152。
实际运行结果为:
make && ./test-trans -M 32 -N 32TEST_TRANS_RESULTS=1:1184发现实际结果高于我们的估计值,这是因为在处理对角线的元素时,A 和 B 映射到相同的缓存块,这将导致格外的缓存冲突未命中。
这显然距离要求有很大距离,我们可以采用分块技术 (blocking) 来减少 miss 数量。具体而言,我们可以将 32 × 32 的矩阵划分成 8 × 8 的小块,再对每个小块依次进行简单的转置。这样一来,B 矩阵的小块在列优先访问时,并不会出现冲突未命中(图中任意连续 8 行无相同颜色)。
void trans_32_32(int M, int N, int A[N][M], int B[M][N])
{
int i, j, k;
int tmp1, tmp2, tmp3, tmp4, tmp5, tmp6, tmp7, tmp8;
for (i = 0; i < N; i += 8) {
for (j = 0; j < M; j += 8) {
for (k = 0; k < 8; ++k) {
tmp1 = A[i+k][j];
tmp2 = A[i+k][j+1];
tmp3 = A[i+k][j+2];
tmp4 = A[i+k][j+3];
tmp5 = A[i+k][j+4];
tmp6 = A[i+k][j+5];
tmp7 = A[i+k][j+6];
tmp8 = A[i+k][j+7];
B[j][i+k] = tmp1;
B[j+1][i+k] = tmp2;
B[j+2][i+k] = tmp3;
B[j+3][i+k] = tmp4;
B[j+4][i+k] = tmp5;
B[j+5][i+k] = tmp6;
B[j+6][i+k] = tmp7;
B[j+7][i+k] = tmp8;
}
}
}
}现在再来估计一下 miss 数量:
- A 矩阵块是行优先访问,可以充分利用整个块,仅在每次装载一个新块时产生 miss,概率为 1/8。
- B 矩阵块是列优先访问,但由于所有块能够填入缓存(无同色),因此仅在对 B 矩阵块第一列的访问时都会产生 miss,后续访问均 hit,概率为 1/8。
综合考虑最终 miss 数量大致为 (32 × 32) × (1/8 + 1/8) = 256。
实际运行结果为:
make && ./test-trans -M 32 -N 32TEST_TRANS_RESULTS=1:288满足要求,高于 256 的部分同样是由于对角线元素造成的。
64 × 64
64 × 64 矩阵的转置要求 miss 数量控制在 1300 以内。首先观察一下矩阵的缓存映射结构。
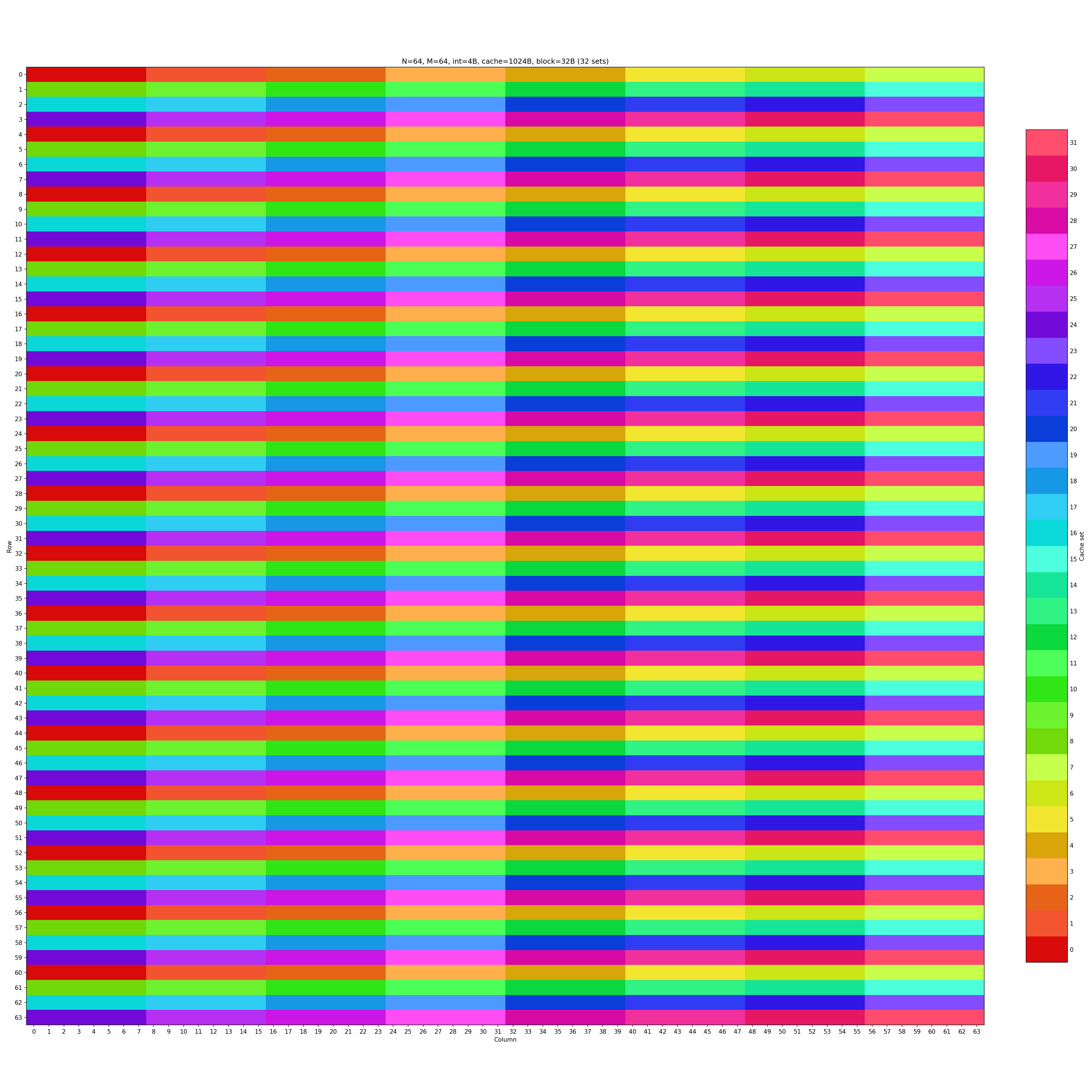
可以看到矩阵不再具有任意连续 8 行不同色的性质了,若我们沿用 8 × 8 的分块方法:
void trans_64_64(int M, int N, int A[N][M], int B[M][N])
{
int i, j, k;
int tmp1, tmp2, tmp3, tmp4, tmp5, tmp6, tmp7, tmp8;
for (i = 0; i < N; i += 8) {
for (j = 0; j < M; j += 8) {
for (k = 0; k < 8; ++k) {
tmp1 = A[i+k][j];
tmp2 = A[i+k][j+1];
tmp3 = A[i+k][j+2];
tmp4 = A[i+k][j+3];
tmp5 = A[i+k][j+4];
tmp6 = A[i+k][j+5];
tmp7 = A[i+k][j+6];
tmp8 = A[i+k][j+7];
B[j][i+k] = tmp1;
B[j+1][i+k] = tmp2;
B[j+2][i+k] = tmp3;
B[j+3][i+k] = tmp4;
B[j+4][i+k] = tmp5;
B[j+5][i+k] = tmp6;
B[j+6][i+k] = tmp7;
B[j+7][i+k] = tmp8;
}
}
}
}简单估计一下产生的 miss 数量:
- A 矩阵块是行优先访问,可以充分利用整个块,仅在每次装载一个新块时产生 miss,概率为 1/8。
- B 矩阵块是列优先访问,但由于所有块能够填入缓存(无同色),因此每次对 B 矩阵块元素的访问都会产生一次 miss,概率为 1。
综合考虑最终 miss 数量大致为 (64 × 64) × (1/8 + 1) = 4608。
实际运行结果为:
make && ./test-trans -M 64 -N 64TEST_TRANS_RESULTS=1:4612这距离要求还有很大差距。
注意到,图中任意连续 4 行无相同颜色,我们可以尝试 4 × 4 的分块方法:
void trans_64_64(int M, int N, int A[N][M], int B[M][N])
{
int i, j, k;
int tmp1, tmp2, tmp3, tmp4;
for (i = 0; i < N; i += 4) {
for (j = 0; j < M; j += 4) {
for (k = 0; k < 4; ++k) {
tmp1 = A[i+k][j];
tmp2 = A[i+k][j+1];
tmp3 = A[i+k][j+2];
tmp4 = A[i+k][j+3];
B[j][i+k] = tmp1;
B[j+1][i+k] = tmp2;
B[j+2][i+k] = tmp3;
B[j+3][i+k] = tmp4;
}
}
}
}简单估计一下产生的 miss 数量:
- A 矩阵块是行优先访问,但是并不能充分利用整个块,但由于我们是以行优先的顺序处理 4 × 4 块的,因此每两次 4 × 4 块处理才会装载新的缓存块,概率依然为 1/8。
- B 矩阵块是列优先访问,但由于所有块能够填入缓存(无同色),因此仅在对 B 矩阵块第一列的访问时都会产生 miss,后续访问均 hit,概率为 1/4。
综合考虑最终 miss 数量大致为 (64 × 64) × (1/8 + 1/4) = 1536。
实际运行结果为:
make && ./test-trans -M 64 -N 64TEST_TRANS_RESULTS=1:1700虽然相比之前大大减少了 miss 数量,但仍未达到要求。
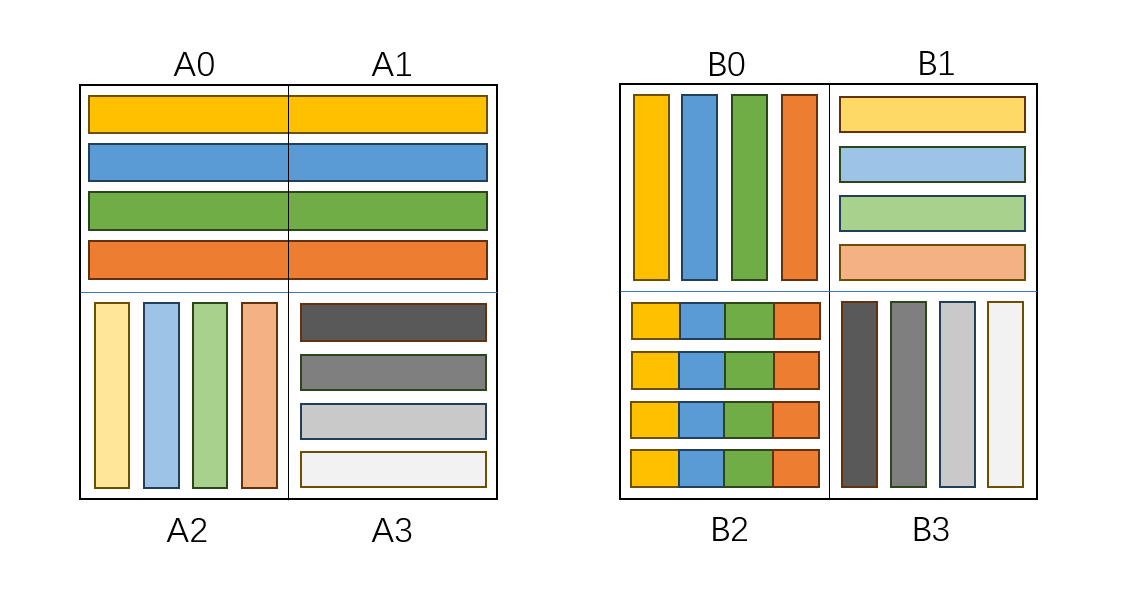
接下来我们采取一种非常巧妙的方法,在 8 × 8 的块中以 4 × 4 的小块为单位完成转置操作。我们将 8 × 8 的块划分成 4 个 4 × 4 的小块,记为 A0,A1,A2,A3 和 B0,B1,B2,B3。
首先,我们以行优先顺序读入 A0 和 A1,这将会占用四个缓存块,产生 4 次 miss。对每行 8 个元素,我们希望将其转置后写入 B 矩阵的对应 8 × 8 块,即 B0 和 B2,但我们先暂时将本应在写入到 B2 的元素写入到 B1,这样可以保证写入操作只占用四个缓存块,产生 4 次 miss。
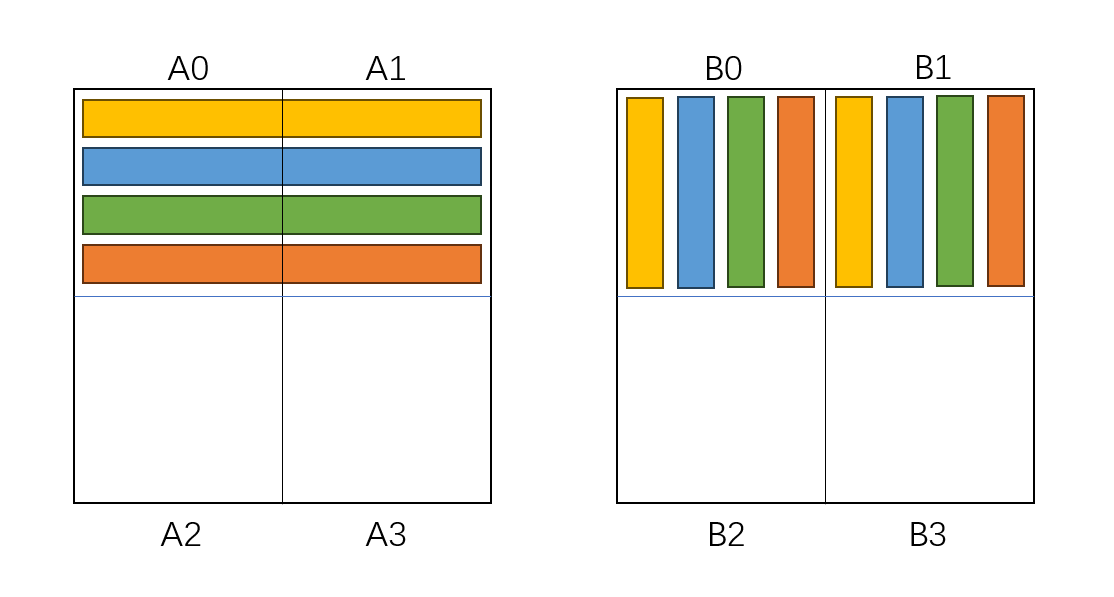
然后,我们以列优先顺序读入 A2,这将会占用四个缓存块,产生 4 次 miss。对每列 4 个元素,我们希望将其转置后写入 B1,但此时 B1 正被本应在 B2 的元素占据,我们需要在写入的同时把 B1 的元素转移到 B2。所以,我们需要 4 个临时变量,在 A2 的单个列写入 B1 的单个行后暂时保存原来行的元素,然后将这 4 个临时变量一起写入 B2 的单个行。写入 B1 的单个行并不会产生 miss,因为对应的缓存块在上一步中就已经被加载到缓存中了,转移 B1 的单个行到 B2 会产生一次 miss,因此总共产生 4 次 miss。
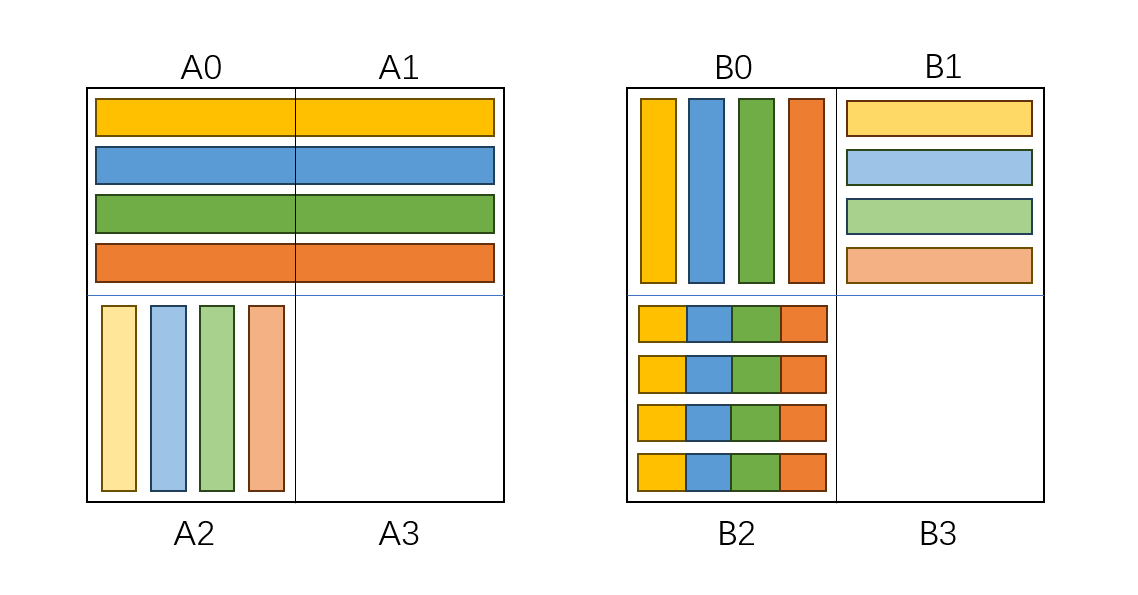
最后,我们以行优先顺序读入 A3,这将会占用四个缓存块,但不会产生 miss,因为对应的缓存块在上一步中就已经被加载到缓存中了。对每行 4 个元素,我们将其转置后写入 B3 的列中,这将占用四个缓存块,但不会产生 miss,因为对应的缓存块在上一步中就已经被加载到缓存中了。
具体代码实现为:
void trans_64_64(int M, int N, int A[N][M], int B[M][N])
{
int i, j, k;
int tmp1, tmp2, tmp3, tmp4, tmp5, tmp6, tmp7, tmp8;
for (i = 0; i < N; i += 8) {
for (j = 0; j < M; j += 8) {
for (k = 0; k < 4; ++k) {
tmp1 = A[i+k][j];
tmp2 = A[i+k][j+1];
tmp3 = A[i+k][j+2];
tmp4 = A[i+k][j+3];
tmp5 = A[i+k][j+4];
tmp6 = A[i+k][j+5];
tmp7 = A[i+k][j+6];
tmp8 = A[i+k][j+7];
B[j][i+k] = tmp1;
B[j+1][i+k] = tmp2;
B[j+2][i+k] = tmp3;
B[j+3][i+k] = tmp4;
B[j][i+k+4] = tmp5;
B[j+1][i+k+4] = tmp6;
B[j+2][i+k+4] = tmp7;
B[j+3][i+k+4] = tmp8;
}
for (k = 0; k < 4; ++k) {
tmp1 = A[i+4][j+k];
tmp2 = A[i+5][j+k];
tmp3 = A[i+6][j+k];
tmp4 = A[i+7][j+k];
tmp5 = B[j+k][i+4];
tmp6 = B[j+k][i+5];
tmp7 = B[j+k][i+6];
tmp8 = B[j+k][i+7];
B[j+k][i+4] = tmp1;
B[j+k][i+5] = tmp2;
B[j+k][i+6] = tmp3;
B[j+k][i+7] = tmp4;
B[j+k+4][i] = tmp5;
B[j+k+4][i+1] = tmp6;
B[j+k+4][i+2] = tmp7;
B[j+k+4][i+3] = tmp8;
}
for (k = 0; k < 4; ++k) {
tmp1 = A[i+k+4][j+4];
tmp2 = A[i+k+4][j+5];
tmp3 = A[i+k+4][j+6];
tmp4 = A[i+k+4][j+7];
B[j+4][i+k+4] = tmp1;
B[j+5][i+k+4] = tmp2;
B[j+6][i+k+4] = tmp3;
B[j+7][i+k+4] = tmp4;
}
}
}
}现在我们简单估计一下产生的 miss 数量:
- 对一个 8 × 8 块的转置操作会产生 16 次 miss。
- 一共有 8 × 8 个矩阵块。
综合考虑最终 miss 数量大致为 (8 × 8) × 16 = 1024。
实际运行结果为:
make && ./test-trans -M 64 -N 64TEST_TRANS_RESULTS=1:1180满足要求!
60 × 68
60 × 68 矩阵转置要求 miss 数量控制在 1600 以内。我们照例观察一下矩阵的缓存映射结构。

相比此前的矩阵而言可谓是非常混乱了,我们首先尝试 4 × 4 的分块方法:
void trans_60_68(int M, int N, int A[N][M], int B[M][N])
{
int i, j, k;
int tmp1, tmp2, tmp3, tmp4;
for (i = 0; i < N; i += 4) {
for (j = 0; j < M; j += 4) {
for (k = 0; k < 4; ++k) {
tmp1 = A[i+k][j];
tmp2 = A[i+k][j+1];
tmp3 = A[i+k][j+2];
tmp4 = A[i+k][j+3];
B[j][i+k] = tmp1;
B[j+1][i+k] = tmp2;
B[j+2][i+k] = tmp3;
B[j+3][i+k] = tmp4;
}
}
}
}简单估计一下产生的 miss 数量:
- A 矩阵块是行优先访问,但是并不能充分利用整个块,但由于我们是以行优先的顺序处理 4 × 4 块的,因此每两次 4 × 4 块处理才会装载新的缓存块,概率依然为 1/8。
- B 矩阵块是列优先访问,但由于所有块能够填入缓存(无同色),因此仅在对 B 矩阵块第一列的访问时都会产生 miss,后续访问均 hit,概率为 1/4。
综合考虑最终 miss 数量大致为 (60 × 68) × (1/8 + 1/4) = 1530。
实际运行结果为:
make && ./test-trans -M 60 -N 68TEST_TRANS_RESULTS=1:1685可以看到已经非常接近要求了。
我们进而尝试 8 × 8 的分块方法,剩余部分划分为 4 × 4 块处理:
void trans_60_68(int M, int N, int A[N][M], int B[M][N])
{
int i, j, k;
int tmp1, tmp2, tmp3, tmp4, tmp5, tmp6, tmp7, tmp8;
for (i = 0; i < 64; i += 8) {
for (j = 0; j < 56; j += 8) {
for (k = 0; k < 8; ++k) {
tmp1 = A[i+k][j];
tmp2 = A[i+k][j+1];
tmp3 = A[i+k][j+2];
tmp4 = A[i+k][j+3];
tmp5 = A[i+k][j+4];
tmp6 = A[i+k][j+5];
tmp7 = A[i+k][j+6];
tmp8 = A[i+k][j+7];
B[j][i+k] = tmp1;
B[j+1][i+k] = tmp2;
B[j+2][i+k] = tmp3;
B[j+3][i+k] = tmp4;
B[j+4][i+k] = tmp5;
B[j+5][i+k] = tmp6;
B[j+6][i+k] = tmp7;
B[j+7][i+k] = tmp8;
}
}
}
for (j = 0; j < 56; j += 4) {
for (k = 0; k < 4; ++k) {
tmp1 = A[64+k][j];
tmp2 = A[64+k][j+1];
tmp3 = A[64+k][j+2];
tmp4 = A[64+k][j+3];
B[j][64+k] = tmp1;
B[j+1][64+k] = tmp2;
B[j+2][64+k] = tmp3;
B[j+3][64+k] = tmp4;
}
}
for (i = 0; i < 68; i += 4) {
for (k = 0; k < 4; ++k) {
tmp1 = A[i+k][56];
tmp2 = A[i+k][57];
tmp3 = A[i+k][58];
tmp4 = A[i+k][59];
B[56][i+k] = tmp1;
B[57][i+k] = tmp2;
B[58][i+k] = tmp3;
B[59][i+k] = tmp4;
}
}
}简单估计一下产生的 miss 数量:
- A 矩阵块是行优先访问,因此共产生 8 次 miss。
- B 矩阵块是列优先访问,在对 B 矩阵块第一列的访问时都会产生 miss,在对 B 矩阵块第五列的访问时会有一般行产生 miss,后续访问均 hit,因此总共产生 12 次 miss。
因此对一个 8 × 8 块的操作会产生 20 次 miss,而分解为 4 个 4 × 4 块会产生共 (8 × 8) × (1/8 + 1/4) = 24 个 miss,理论上优于上一种方案。
实际运行结果为:
make && ./test-trans -M 60 -N 68TEST_TRANS_RESULTS=1:1617非常可惜,距离要求只有一步之遥。
接下来,我们可以选择在 B 中进行转置操作来进一步优化,具体操作是将 A 矩阵块按行依次原封不动的转移到 B 矩阵对应的块中,然后再在 B 矩阵块中对除对角线外的元素进行转置操作。
void trans_60_68(int M, int N, int A[N][M], int B[M][N])
{
int i, j, k, l;
int tmp1, tmp2, tmp3, tmp4, tmp5, tmp6, tmp7, tmp8;
for (i = 0; i < 64; i += 8) {
for (j = 0; j < 56; j += 8) {
for (k = 0; k < 8; ++k) {
tmp1 = A[i+k][j];
tmp2 = A[i+k][j+1];
tmp3 = A[i+k][j+2];
tmp4 = A[i+k][j+3];
tmp5 = A[i+k][j+4];
tmp6 = A[i+k][j+5];
tmp7 = A[i+k][j+6];
tmp8 = A[i+k][j+7];
B[j+k][i] = tmp1;
B[j+k][i+1] = tmp2;
B[j+k][i+2] = tmp3;
B[j+k][i+3] = tmp4;
B[j+k][i+4] = tmp5;
B[j+k][i+5] = tmp6;
B[j+k][i+6] = tmp7;
B[j+k][i+7] = tmp8;
}
for (k = 0; k < 8; ++k) {
for (l = 0; l < k; ++l) {
tmp1 = B[j+k][i+l];
B[j+k][i+l] = B[j+l][i+k];
B[j+l][i+k] = tmp1;
}
}
}
}
for (j = 0; j < 56; j += 4) {
for (k = 0; k < 4; ++k) {
tmp1 = A[64+k][j];
tmp2 = A[64+k][j+1];
tmp3 = A[64+k][j+2];
tmp4 = A[64+k][j+3];
B[j+k][64] = tmp1;
B[j+k][65] = tmp2;
B[j+k][66] = tmp3;
B[j+k][67] = tmp4;
}
for (k = 0; k < 4; ++k) {
for (l = 0; l < k; ++l) {
tmp1 = B[j+k][64+l];
B[j+k][64+l] = B[j+l][64+k];
B[j+l][64+k] = tmp1;
}
}
}
for (i = 0; i < 68; i += 4) {
for (k = 0; k < 4; ++k) {
tmp1 = A[i+k][56];
tmp2 = A[i+k][57];
tmp3 = A[i+k][58];
tmp4 = A[i+k][59];
B[56+k][i] = tmp1;
B[56+k][i+1] = tmp2;
B[56+k][i+2] = tmp3;
B[56+k][i+3] = tmp4;
}
for (k = 0; k < 4; ++k) {
for (l = 0; l < k; ++l) {
tmp1 = B[56+k][i+l];
B[56+k][i+l] = B[56+l][i+k];
B[56+l][i+k] = tmp1;
}
}
}
}简单估计一下产生的 miss 数量:
- A 矩阵块读入操作共产生 8 次 miss。
- B 矩阵块写入操作共产生 8 次 miss。
- 对 B 矩阵块的转置操作不会产生 miss,因为 B 矩阵块中的元素都已经加载到缓存中。
因此对一个 8 × 8 块的操作会产生 16 次 miss,理论上优于上一种方案。
实际运行结果为:
make && ./test-trans -M 60 -N 68TEST_TRANS_RESULTS=1:1566顺利满足要求!
最后整合对三种矩阵的针对性处理,在 transpose_submit 中根据不同的情形调用三个函数:
char transpose_submit_desc[] = "Transpose submission";
void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
if (M == 32 && N == 32)
trans_32_32(M, N, A, B);
else if (M == 64 && N == 64)
trans_64_64(M, N, A, B);
else if (M == 60 && N == 68)
trans_60_68(M, N, A, B);
}编译并测试:
make && python3 ./driver.pyPart A: Testing cache simulator
Running ./test-csim
Your simulator Reference simulator
Points (s,E,b) Hits Misses Evicts Hits Misses Evicts
3 (1,1,1) 11 8 6 11 8 6 traces/yi2.trace
3 (4,2,4) 4 5 2 4 5 2 traces/yi.trace
3 (2,1,4) 2 3 1 2 3 1 traces/dave.trace
3 (2,1,3) 694 453 449 694 453 449 traces/mem.trace
3 (2,2,3) 201 37 29 201 37 29 traces/trans.trace
3 (2,4,3) 212 26 10 212 26 10 traces/trans.trace
3 (5,1,5) 231 7 0 231 7 0 traces/trans.trace
6 (5,1,5) 265189 21777 21745 265189 21777 21745 traces/long.trace
27
Part B: Testing transpose function
Running ./test-trans -M 32 -N 32
Running ./test-trans -M 64 -N 64
Running ./test-trans -M 60 -N 68
Cache Lab summary:
Points Max pts Misses
Csim correctness 27.0 27
Trans perf 32x32 8.0 8 288
Trans perf 64x64 8.0 8 1180
Trans perf 60x68 10.0 10 1566
Total points 53.0 53
Final points 88.0 88至此完成 Cache Lab。