弹性力学问题的基本解法包括位移解法、应力解法和应力函数解法等。位移解法以位移分量为基本未知量，将几何方程和本构关系代入平衡方程，得到关于位移的偏微分方程组（拉梅-纳维方程）；应力解法以应力分量为基本未知量，将本构关系代入应变协调方程，得到关于应力的偏微分方程组（贝尔脱拉密-密乞尔方程）；应力函数解法则是引入适当应力函数，使平衡方程自动满足，仅需解关于应力函数的偏微分方程及相应边界条件。

除基本解法外，实际求解过程中常采用逆解法和半逆解法等求解方式。逆解法是先假设满足基本微分方程的一组解，再反推出这个解对应的边界载荷性质；半逆法则是根据边界条件特点或对域内应力应变状态的定性估计，假设一个能满足部分边界条件的解函数形式，再调整待定成分使满足全部方程和边界条件。

本章将系统介绍应力函数解法，并通过平面问题的直角坐标和极坐标解法展示该方法的应用。

注

本章的所有讨论均基于二维弹性力学问题，且认为介质具有各向同性。

1 应力函数

1.1 应力函数的基本概念

二维问题的平衡方程为

$$\frac{\partial \sigma_x}{\partial x} + \frac{\partial \tau_{xy}}{\partial y} = f_x,\quad \frac{\partial \tau_{xy}}{\partial x} + \frac{\partial \sigma_y}{\partial y} = f_y$$

若体力有势（$f_x = -\frac{\partial V}{\partial x}, f_y = -\frac{\partial V}{\partial y}$），则可引入艾里（Airy）应力函数 $\phi(x,y)$，使

$$\sigma_x = \frac{\partial^2 \phi}{\partial y^2} + V,\quad \sigma_y = \frac{\partial^2 \phi}{\partial x^2} + V,\quad \tau_{xy} = -\frac{\partial^2 \phi}{\partial x \partial y}$$

这样，平衡方程便自动满足。

1.2 使用应力函数的应力解法

将应力函数表达式代入平面问题的应力协调方程可得

• 平面应变问题

  $$\nabla^4 \phi = -\frac{1-2\nu}{1-\nu}\nabla^2V$$

• 平面应力问题

  $$\nabla^4 \phi = (\nu-1)\nabla^2V$$

对于无体力或常体力情况，二者形式相同，为重调和方程

$$\nabla^4 \phi = 0$$

注

本章后续的讨论，均默认为无体力或常体力情况，对重调和方程进行求解。

应力函数法将求解应力协调方程和平衡方程的问题，转换为求解一个四阶偏微分方程。

1.3 应力函数的性质

性质1：可加性

应力函数可确定到只差一个线性函数的程度。

$$\phi = \phi_0 + ax + by + c$$

其中 $a$, $b$, $c$ 为任意常数。由于应力是应力函数的二阶导数，线性项不影响应力分布。

性质2：边界性质

在边界上，应力函数及其一阶导数的值由边界载荷的主矩和主矢量确定。

以边界上某点 A 为参考点，令 $\phi_A = 0$，$\left.\frac{\partial \phi}{\partial x}\right|_A = 0$，$\left.\frac{\partial \phi}{\partial y}\right|_A = 0$（这可以由添加线性函数做到），则在任意边界点B处

$$\phi_B = M_B,\quad \frac{\partial \phi}{\partial x}\bigg|_B = -R_y,\quad \frac{\partial \phi}{\partial y}\bigg|_B = R_x$$

其中 $M_B$ 为 AB 段边界载荷对 B 点的力矩，$R_x$ 和 $R_y$ 分别为 AB 段边界载荷在 $x$ 和 $y$ 方向的合力分量。

注

上式中边界走向严格为逆时针，$R_x$ 和 $R_y$ 均以坐标轴正向为正，采用右手系。

应力函数边界性质示意图

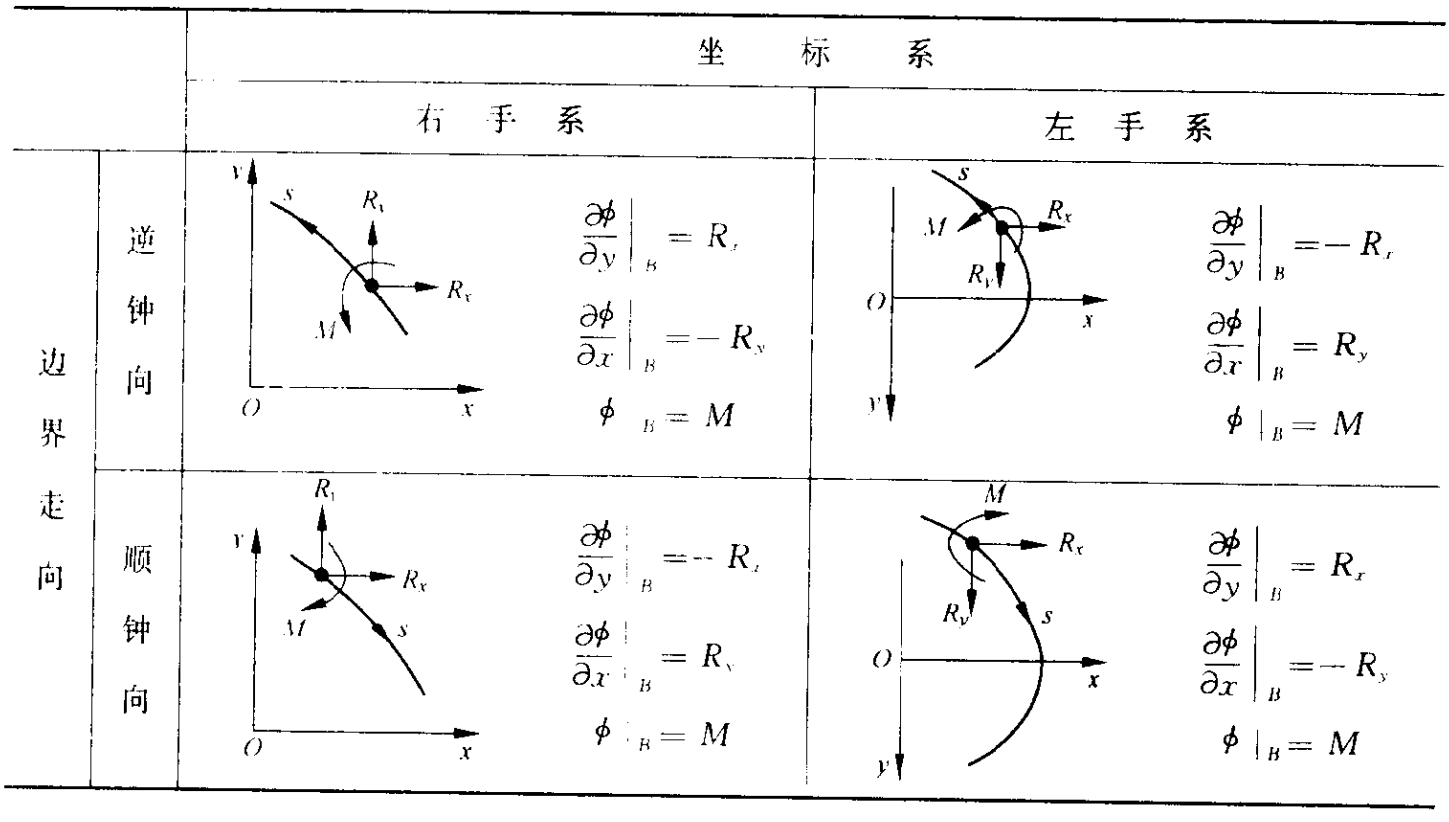
性质3：单值条件

应力函数的单值条件是：作用在物体一个闭合界面上的全部载荷构成自平衡力系。

平面问题的面内载荷都是自平衡力系，所以单连体内的应力函数必定单值。多连体有多个闭合边界，每边所受的载荷不一定自平衡，因而应力函数可能多值，但多值性仅影响 $\phi$ 及其一阶导数，应力仍是单值的。

2 平面问题的直角坐标解法

将应力函数 $\phi$ 表示成多项式形式：

$$\phi = a_0 + a_1x + b_1y + a_2x^2 + b_2xy + c_2y^2 + a_3x^3 + b_3x^2y + c_3xy^2 + d_3y^3 + \cdots$$

其中，低于四次的项自动满足重调和方程，因此对于无体力或常体力问题，可以采用半逆解法，利用边界条件反解系数。

二次项：

• $\phi = ax^2$ $\Rightarrow$ $\sigma_x = 0$, $\sigma_y = 2a$, $\tau_{xy} = 0$（单向拉伸状态）
• $\phi = by^2$ $\Rightarrow$ $\sigma_x = 2b$, $\sigma_y = 0$, $\tau_{xy} = 0$（单向拉伸状态）
• $\phi = cxy$ $\Rightarrow$ $\sigma_x = 0$, $\sigma_y = 0$, $\tau_{xy} = -c$（纯剪切状态）

三次项：

• $\phi = ax^3$ $\Rightarrow$ $\sigma_x = 0$, $\sigma_y = 6ax$, $\tau_{xy} = 0$
• $\phi = bx^2y$ $\Rightarrow$ $\sigma_x = 0$, $\sigma_y = 2by$, $\tau_{xy} = -2bx$
• $\phi = cxy^2$ $\Rightarrow$ $\sigma_x = 2cx$, $\sigma_y = 0$, $\tau_{xy} = -2cy$
• $\phi = dy^3$ $\Rightarrow$ $\sigma_x = 6dy$, $\sigma_y = 0$, $\tau_{xy} = 0$

3 平面问题的极坐标解法

3.1 极坐标系下的控制方程

在极坐标 $(r,\theta)$ 下，控制方程的形式产生变化：

• 平衡方程

$$\frac{\partial \sigma_r}{\partial r} + \frac{1}{r}\frac{\partial \tau_{r\theta}}{\partial \theta} + \frac{\sigma_r - \sigma_\theta}{r} + f_r = 0$$

$$\frac{\partial \tau_{r\theta}}{\partial r} + \frac{1}{r}\frac{\partial \sigma_\theta}{\partial \theta} + \frac{2\tau_{r\theta}}{r} + f_\theta = 0$$

• 几何方程

$$\varepsilon_r = \frac{\partial u_r}{\partial r},\quad \varepsilon_\theta = \frac{1}{r}\frac{\partial u_\theta}{\partial \theta} + \frac{u_r}{r},\quad \gamma_{r\theta} = \frac{1}{r}\frac{\partial u_r}{\partial \theta} + \frac{\partial u_\theta}{\partial r} - \frac{u_\theta}{r}$$

• 本构方程

  $$x\rightarrow r,\quad y\rightarrow \theta$$

除此之外，应力函数的定义以及重调和方程的形式变为：

$$\sigma_r = \frac{1}{r}\frac{\partial \phi}{\partial r} + \frac{1}{r^2}\frac{\partial^2 \phi}{\partial \theta^2},\quad \sigma_\theta = \frac{\partial^2 \phi}{\partial r^2},\quad \tau_{r\theta} = -\frac{\partial}{\partial r}\left(\frac{1}{r}\frac{\partial \phi}{\partial \theta}\right)$$

$$\left(\frac{\partial^2}{\partial r^2} + \frac{1}{r}\frac{\partial}{\partial r} + \frac{1}{r^2}\frac{\partial^2}{\partial \theta^2}\right)^2 \phi = 0$$

3.2 平面轴对称问题

几何形状和载荷分布都与环向坐标 $\theta$ 无关的平面问题称为平面轴对称问题。应力函数简化为 $\phi = \phi(r)$，重调和方程变为：

$$\left(\frac{d^2}{dr^2} + \frac{1}{r}\frac{d}{dr}\right)^2 \phi = 0$$

解得：

$$\phi = A\ln r + Br^2\ln r + Cr^2 + D$$

应力分量为：

$$\sigma_r = B(1+2\ln r) + 2C + A/r^2\\ \sigma_\theta = B(3+2\ln r) + 2C - A/r^2\\ \tau_{r\theta} = 0$$

实心圆筒问题

半径为 $R$ 的实心圆筒，外壁受压 $p$。因此边界条件为

$$\sigma_r\bigg|_{r=R} = -p,\quad \tau_{r\theta}\bigg|_{r=R} = 0$$

实心圆筒为一个单连体，因此要求应力函数为单值，所以有

$$A=B=0$$

带入边界条件解得

$$C=-p/2$$

故

$$\sigma_r = -p,\quad \sigma_\theta = 0,\quad \tau_{r\theta} = 0$$

厚壁圆筒问题

内外半径分别为 $a$ 和 $b$ 的圆筒，内壁受压 $p_i$，外壁受压 $p_o$。因此边界条件为

$$\sigma_r\bigg|_{r=b} = -p_o,\quad \tau_{r\theta}\bigg|_{r=b} = 0\\ \sigma_r\bigg|_{r=a} = -p_i,\quad \tau_{r\theta}\bigg|_{r=a} = 0$$

厚壁圆筒为一个多连体，因此由应力协调方程不能推出位移单值连续，需要引入格外的约束。

由本构关系得

$$\varepsilon_r=K_1(\sigma_r-K_2\sigma_\theta)\\ \varepsilon_\theta=K_1(\sigma_\theta-K_2\sigma_r)\\ \varepsilon_{r\theta}=0$$

注

$K_1,K_2$ 为常系数，由平面应变/应力问题决定。

对应变积分得到位移的表达式为

$$u_r=K_1\left[-(1+K_2)\frac{A}{r}+2(1-K_2)Br\ln r -(1+K_2)Br+2(1-K_2)Cr\right]+I\cos\theta+K\sin\theta\\ u_\theta=4K_1Br\theta+Hr+K\cos\theta-I\sin\theta$$

位移单值条件要求 $B=0$，于是

$$\sigma_r = 2C + A/r^2\\ \sigma_\theta = 2C - A/r^2\\ \tau_{r\theta} = 0$$

$$u_r=K_1\left[-(1+K_2)\frac{A}{r}+2(1-K_2)Cr\right]+I\cos\theta+K\sin\theta\\ u_\theta=Hr+K\cos\theta-I\sin\theta$$

注

$I$ 和 $K$ 对应刚体的位移，$H$ 对应刚体的转动。

其中常数 $A$ 和 $C$ 可由力边界条件或位移边界条件确定。最终解得

$$\sigma_r = \frac{a^2p_i-b^2p_o}{b^2 - a^2} - \frac{(p_i - p_o)a^2b^2}{(b^2 - a^2)r^2}$$

$$\sigma_\theta = \frac{a^2p_i-b^2p_o}{b^2 - a^2} + \frac{(p_i - p_o)a^2b^2}{(b^2 - a^2)r^2}$$

$$\tau_{r\theta} = 0$$

这便是著名的拉梅（Lame）公式。它与弹性常数无关，因而同时适用于两类平面问题。

3.3 平面非轴对称问题：圆孔的应力集中

考虑无限大的薄板中有一半径为 $a$ 的小圆孔，$x$ 方向受拉力 $p$，$y$ 方向受拉力 $q$。

考虑一半径为 $b$ 的圆孔的同心圆（$b \gg a$），由圣维南原理，同心圆上的应力状态可以认为和无小孔的薄板时的情形相同，将其写为极坐标形式，即

$$\sigma_r\bigg|_{r=b} = \frac{p+q}{2}+\frac{p-q}{2}\cos2\theta\\ \tau_{r\theta}\bigg|_{r=b} = -\frac{p-q}{2}\sin2\theta$$

故问题可以转化为两个厚壁圆筒问题的叠加，其边界条件为

$$\sigma_r^1\bigg|_{r=b} = \frac{p+q}{2},\quad \tau^1_{r\theta}\bigg|_{r=b} = 0\\ \sigma_r^1\bigg|_{r=a} = 0,\quad \tau^1_{r\theta}\bigg|_{r=a} = 0$$

注

等向拉伸（或压缩）情形

以及

$$\sigma^2_r\bigg|_{r=b} = \frac{p-q}{2}\cos2\theta,\quad \tau^2_{r\theta}\bigg|_{r=b} = -\frac{p-q}{2}\sin2\theta\\ \sigma^2_r\bigg|_{r=a} = 0,\quad \tau^2_{r\theta}\bigg|_{r=a} = 0$$

注

等值拉压情形

对于第一个厚壁圆筒问题，代入拉梅公式，再令 $b\rightarrow +\infty$ 得

$$\sigma^1_r = \frac{p+q}{2}\left(1-\frac{a^2}{r^2}\right)$$

$$\sigma^1_\theta = \frac{p+q}{2}\left(1+\frac{a^2}{r^2}\right)$$

$$\tau^1_{r\theta} = 0$$

对于第二个厚壁圆筒问题，采用半逆解法，设应力函数为

$$\phi = f(r)\cos 2\theta$$

代入重调和方程，解得：

$$f(r) = Ar^4 + Br^2 + C + Dr^{-2}$$

根据边界条件反解出 $A,B,C,D$ 代入应力表达式，再令 $b\rightarrow +\infty$ 得

$$\sigma^2_r = \frac{p-q}{2}\left(1 - \frac{a^2}{r^2}\right)\left(1 - 3\frac{a^2}{r^2}\right)\cos 2\theta$$

$$\sigma^2_\theta = -\frac{p-q}{2}\left(1 + 3\frac{a^4}{r^4}\right)\cos 2\theta$$

$$\tau^2_{r\theta} = -\frac{p-q}{2}\left(1 - \frac{a^2}{r^2}\right)\left(1 + 3\frac{a^2}{r^2}\right)\sin 2\theta$$

在孔边 $r = a$ 上，当 $\theta = \pi/2$ 和 $3\pi/2$ 时，$\sigma_\theta$ 的应力集中系数为 $k = 4$，当 $\theta = 0$ 和 $\pi$ 时，$k=-4$。

3.4 空间问题：圆柱体的扭转

圆柱体长为 $L$，半径为 $a$，绕 $z$ 轴轴对称，上下表面受一对大小为 $M$ 的反向力矩作用，圆柱体整体无位移和旋转。

示意图

采用以下假设：

• 刚性转动假设：横截面绕轴线刚性旋转，其形状和大小保持不变。

  注

  设 $\beta=\alpha z$，其中 $\alpha$ 为常系数，$\beta$ 为旋转弧度。

• 等翘曲假设：所有横截面的纵向翘曲位移模式相同，与轴向位置无关。

  注

  设 $w=w(x,y)$。

3.4.1 微分方程

使用半逆解法，设位移为

$$u=-\alpha yz\\ v=\alpha xz\\ w=w(x,y)$$

由几何关系，应变为

$$\gamma_{xz}=\frac{\partial w}{\partial x}-\alpha y,\quad \gamma_{yz}=\frac{\partial w}{\partial y}-\alpha x\\ \varepsilon_x=\varepsilon_y=\varepsilon_z=\gamma_{xy}=0$$

由本构关系，应力为

$$\tau_{xz}=G(\frac{\partial w}{\partial x}-\alpha y),\quad \tau_{yz}=G(\frac{\partial w}{\partial y}-\alpha x)\\ \sigma_x=\sigma_y=\sigma_z=\tau_{xy}=0$$

则控制方程简化为

$$\frac{\partial\tau_{xz}}{\partial y}-\frac{\partial\tau_{yz}}{\partial x}=-2G\alpha \tag{a}$$

$$\frac{\partial\tau_{xz}}{\partial x}+\frac{\partial\tau_{yz}}{\partial y}=0 \tag{b}$$

引入 Prandtl 应力函数 $\phi$，满足

$$\tau_{xz}=\frac{\partial \phi}{\partial y},\quad \tau_{yz}=-\frac{\partial \phi}{\partial x}$$

则 (b) 式自动满足，代入 (a) 式得 Possion 方程

$$\nabla^2 \phi = -2G\alpha$$

4.3.2 边界条件

侧面：

$$T^{\hat{n}}_x=0\\ T^{\hat{n}}_y=0\\ T^{\hat{n}}_z=0$$

其中两式已满足，剩下

$$\tau_{xz}n_x+\tau_{yz}n_y=0$$

上式可以理解为

$$0=\frac{\text{d}x}{\text{d}S}\frac{\partial\phi}{\partial x}+\frac{\text{d}y}{\text{d}S}\frac{\partial\phi}{\partial y}=\frac{\text{d}\phi}{\text{d} S}$$

其中 $\text{d} S$ 是横截面边界上的微元，故 $\phi$ 在任一截面的边界上都为常数，由于常数对于应力无影响，不妨设为 0。

上下端面：

$$\iint_A (T_y^{\hat{n}}x - T_x^{\hat{n}}y)\text{d}x\text{d}y = \mp M$$

上式左边可以转化为

$$\begin{align} \iint_A (T_y^{\hat{n}}x - T_x^{\hat{n}}y)\text{d}x\text{d}y &=\iint_A (\tau_{yz}x - \tau_{xz}y)\text{d}x\text{d}y\\ &=\iint_A (-\frac{\partial \phi}{\partial x}x -\frac{\partial \phi}{\partial y}y)\text{d}x\text{d}y\\ &=\int_y \left(-\phi x\bigg|_{x=x_1}^{x=x_2} + \int_x \phi \text{d}x \right)\text{d}y + \int_x \left(-\phi y\bigg|_{y=y_1}^{y=y_2} + \int_y \phi \text{d}y \right)\text{d}x \\ &=2\iint_A \phi \text{d}x\text{d}y \end{align}$$

4.3.3 问题的解

经过上述讨论问题转化为：

$$\begin{cases} \nabla^2 \phi = -2G\alpha\\ \\ \phi\bigg|_S=0,\quad 2\iint_A \phi \text{d}x\text{d}y = \mp M \end{cases}$$

设

$$\phi=k(x^2+y^2-a^2)$$

代入方程解得 $\alpha=\frac{2M}{\pi a^4 G}$

$$\phi=-\frac{M}{\pi a^4}(x^2+y^2-a^2)$$

$$\tau_{xz}=-\frac{2My}{\pi a^4},\quad \tau_{yz}=-\frac{2Mx}{\pi a^4}$$

进一步求位移

$$u=-\frac{2M}{\pi a^4 G}yz,\quad v=\frac{2M}{\pi a^4 G}xz$$

由几何关系可得到

$$\frac{\partial w}{\partial x}=\frac{\partial w}{\partial y}=0 \Rightarrow w=0$$

注

对于椭圆柱体，仍有相同的边界条件，可设

$$\phi = k(x^2/a^2+y^2/b^2-1)$$

此时有

$$w=\frac{b^2-a^2}{b^2+a^2}xy$$

版权所有

版权归属：Staaaaaaaaar

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)

编辑此页

贡献者: Staaaaaaaaar

上一页第四章：弹性力学定解问题

下一页第六章：能量方法