Sam's Blog

简体中文

English

简体中文

English

外观

第一章：应力分析

约 1575 字大约 5 分钟

2026-01-28

1 应力概念

1.1 外力与内力

  • 外力：作用于物体表面或贯穿体积的载荷，分为：

    • 体力（体积力）：作用于物体内部单位体积上的力（如重力、惯性力、电磁力），记为

      f=lim⁡ΔV→0ΔFΔV,fi=lim⁡ΔV→0ΔFiΔV\mathbf{f} = \lim_{\Delta V \to 0} \frac{\Delta \mathbf{F}}{\Delta V}, \quad f_i = \lim_{\Delta V \to 0} \frac{\Delta F_i}{\Delta V}

    • 面力（表面力）：作用于物体表面单位面积上的力（如液体压力、接触力），记为

      p=lim⁡ΔS→0ΔGΔS,pi=lim⁡ΔS→0ΔGiΔS\mathbf{p} = \lim_{\Delta S \to 0} \frac{\Delta \mathbf{G}}{\Delta S}, \quad p_i = \lim_{\Delta S \to 0} \frac{\Delta G_i}{\Delta S}

  • 内力：外力引起物体变形，破坏分子平衡，从而在物体内部产生抵抗变形的附加相互作用力场，称为附加内力场。

1.2 应力的定义

考虑物体内一点 PP，取任意法向为 ν=νiei\boldsymbol{\nu} = \nu_i \mathbf{e}_i 的截面微元 ΔS\Delta S，该截面一侧物体对另一侧物体的作用合力为 ΔF\Delta \mathbf{F}，则定义应力矢量为：

Tν=lim⁡ΔS→0ΔFΔS\bold{T}^{\boldsymbol{\nu}} = \lim_{\Delta S \to 0} \frac{\Delta \mathbf{F}}{\Delta S}

注

应力是单位面积上的附加内力，是描述连续介质内部受力状态的基本物理量。

2 应力表示

2.1 应力张量

取笛卡儿坐标系，围绕点 PP 作六面微元体。

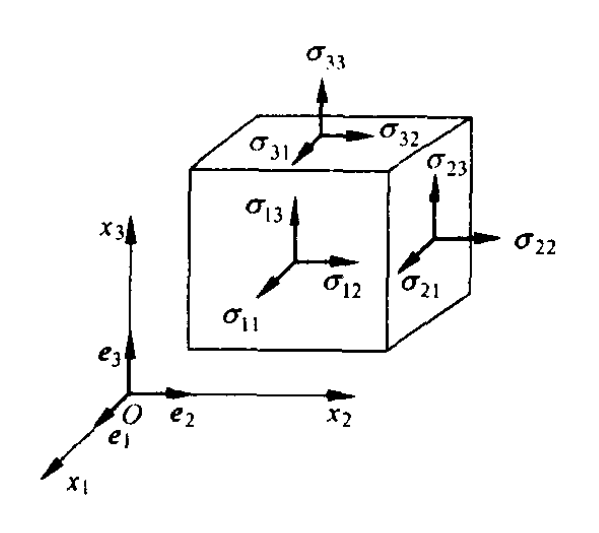
应力张量示意图
应力张量示意图

在三个正面（外法线方向为 e1,e2,e3\mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3）上分解应力矢量：

Te1=σ11e1+σ12e2+σ13e3=σ1jejTe2=σ21e1+σ22e2+σ23e3=σ2jejTe3=σ31e1+σ32e2+σ33e3=σ3jej\begin{aligned} \bold{T}^{\bold{e_1}} &= \sigma_{11}\mathbf{e}_1 + \sigma_{12}\mathbf{e}_2 + \sigma_{13}\mathbf{e}_3 = \sigma_{1j}\mathbf{e}_j \\ \bold{T}^{\bold{e_2}} &= \sigma_{21}\mathbf{e}_1 + \sigma_{22}\mathbf{e}_2 + \sigma_{23}\mathbf{e}_3 = \sigma_{2j}\mathbf{e}_j \\ \bold{T}^{\bold{e_3}} &= \sigma_{31}\mathbf{e}_1 + \sigma_{32}\mathbf{e}_2 + \sigma_{33}\mathbf{e}_3 = \sigma_{3j}\mathbf{e}_j \end{aligned}

由此定义 9 个应力分量，组成应力张量：

[σ]=[σ11σ12σ13σ21σ22σ23σ31σ32σ33][\boldsymbol{\sigma}] = \begin{bmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{bmatrix}

  • 第一下标 ii：作用面法线方向（面元指标）
  • 第二下标 jj：应力投影方向（方向指标）
  • 正应力（法向应力）：σii\sigma_{ii}
  • 剪应力（切向应力）：σij (i≠j)\sigma_{ij}\,(i\neq j)

2.2 正负号约定

  • 正面（法向与坐标轴同向）：应力分量与坐标轴正向一致为正
  • 负面（法向与坐标轴反向）：应力分量与坐标轴反向为正

注

此约定主要是为了满足拉为正、压为负且使得数学处理统一简洁。

3 应力性质

3.1 剪应力互等定理

σij=σji[σ]T=[σ]\sigma_{ij} = \sigma_{ji} \quad [\boldsymbol{\sigma}]^T = [\boldsymbol{\sigma}]

3.2 应力的坐标变换（张量性质）

设新旧坐标系方向余弦为 αmi=cos⁡(xm′,xi)\alpha_{mi} = \cos(x'_m, x_i)，应力分量满足二阶张量分量变换律：

σmn′=αmiαnjσij\sigma'_{mn} = \alpha_{mi} \alpha_{nj} \sigma_{ij}

矩阵形式为：

[σ′]=[α][σ][α]T[\boldsymbol{\sigma}'] = [\boldsymbol{\alpha}] [\boldsymbol{\sigma}] [\boldsymbol{\alpha}]^T

基于这种变换关系，我们可以得到某一点处任一方向上的应力：

Tn^=σ⋅n^\bold{T}^{\bold{\hat{n}}} = \boldsymbol{\sigma}\cdot\bold{\hat{n}}

因此一个点的应力状态可以由应力张量完全表示。

4 主应力

4.1 定义

  • 主平面：仅含正应力、剪应力为零的平面。

  • 主方向：主平面法向 v\boldsymbol{v}，应满足

    [σ]v=λv[\boldsymbol{\sigma}] \boldsymbol{v} = \lambda \boldsymbol{v}

​ 其中 λ\lambda 为一常数（特征值），通常用 σ1,σ2,σ3\sigma_1,\sigma_2,\sigma_3 表示。

  • 主应力：主方向上的（正）应力大小。

注

可通过解特征方程求得主方向和主应力大小，细节参考线性代数。

4.2 应力不变量

与坐标系无关的三个标量：

I1=σ11+σ22+σ33=σkk=tr([σ])I2=σ11σ22+σ22σ33+σ33σ11−(σ122+σ232+σ312)I3=det⁡([σ])\begin{aligned} I_1 &= \sigma_{11} + \sigma_{22} + \sigma_{33} = \sigma_{kk} = \mathrm{tr}([\boldsymbol{\sigma}]) \\ I_2 &= \sigma_{11}\sigma_{22} + \sigma_{22}\sigma_{33} + \sigma_{33}\sigma_{11} - (\sigma_{12}^2 + \sigma_{23}^2 + \sigma_{31}^2) \\ I_3 &= \det([\boldsymbol{\sigma}]) \end{aligned}

4.3 主应力性质

  • 存在性：对称实矩阵必定存在特征值。
  • 正交性：不同主应力对应主方向相互正交，重根时可在对应平面任选正交主方向。

4.4 主坐标系简化

在主方向为坐标轴的坐标系中，应力张量对角化：

[σ]=[σ1000σ2000σ3][\boldsymbol{\sigma}] = \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \end{bmatrix}

不变量简化为：

I1=σ1+σ2+σ3,I2=σ1σ2+σ2σ3+σ3σ1,I3=σ1σ2σ3I_1 = \sigma_1 + \sigma_2 + \sigma_3,\quad I_2 = \sigma_1\sigma_2 + \sigma_2\sigma_3 + \sigma_3\sigma_1,\quad I_3 = \sigma_1\sigma_2\sigma_3

5 莫尔圆

5.1 二维莫尔圆

二维情形下的正应力大小 σ\sigma 和剪应力大小 τ\tau 满足以下关系：

(σ−σ1+σ22)2+τ2=(σ1−σ22)2\left(\sigma - \frac{\sigma_1 + \sigma_2}{2}\right)^2 + \tau^2 = \left(\frac{\sigma_1 - \sigma_2}{2}\right)^2

其中 σ1≥σ2\sigma_1 \ge \sigma_2 ，为主应力大小。

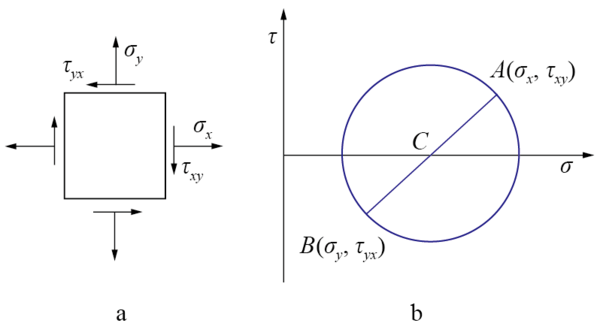
二维莫尔圆示意图
二维莫尔圆示意图

规定莫尔圆中剪应力 τ\tau 以顺时针方向为正，由此将某一点的应力状态投射到了一个圆上。每一个法向上的正应力和剪应力大小就对应莫尔圆上的一个 (σ,τ)(\sigma,\tau) 坐标，法向逆时针旋转 α\alpha ，对应莫尔圆上的点逆时针旋转 2α2\alpha。

5.2 三维莫尔圆

取主轴坐标系，定义法向 n^=(n1,n2,n3)\boldsymbol{\hat{n}}=(n_1,n_2,n_3)，可推出以下三个方程：

(σ−σ2+σ32)2+τ2=(σ2−σ32)2+n12(σ1−σ2)(σ1−σ3)(σ−σ3+σ12)2+τ2=(σ1−σ32)2+n22(σ2−σ1)(σ2−σ3)(σ−σ1+σ22)2+τ2=(σ1−σ22)2+n32(σ3−σ1)(σ3−σ2)\displaystyle \left(\sigma-\frac{\sigma_2+\sigma_3}{2}\right)^2+\tau^2=\left(\frac{\sigma_2-\sigma_3}{2}\right)^2+n_1^2(\sigma_1-\sigma_2)(\sigma_1-\sigma_3) \\ \displaystyle \left(\sigma-\frac{\sigma_3+\sigma_1}{2}\right)^2+\tau^2=\left(\frac{\sigma_1-\sigma_3}{2}\right)^2+n_2^2(\sigma_2-\sigma_1)(\sigma_2-\sigma_3) \\ \displaystyle \left(\sigma-\frac{\sigma_1+\sigma_2}{2}\right)^2+\tau^2=\left(\frac{\sigma_1-\sigma_2}{2}\right)^2+n_3^2(\sigma_3-\sigma_1)(\sigma_3-\sigma_2)

其中 σ1≥σ2≥σ3\sigma_1 \ge \sigma_2 \ge \sigma_3 ，为主应力大小。

绘制三个主平面对应的二维莫尔圆：

  • 圆 C1C_1（σ2\sigma_2–σ3\sigma_3 平面）：圆心 (σ2+σ32,0)\left(\dfrac{\sigma_2+\sigma_3}{2},0\right)，半径 R1=σ2−σ32R_1 = \dfrac{\sigma_2 - \sigma_3}{2}
  • 圆 C2C_2（σ1\sigma_1–σ3\sigma_3 平面）：圆心 (σ1+σ32,0)\left(\dfrac{\sigma_1+\sigma_3}{2},0\right)，半径 R2=σ1−σ32R_2 = \dfrac{\sigma_1 - \sigma_3}{2}
  • 圆 C3C_3（σ1\sigma_1–σ2\sigma_2 平面）：圆心 (σ1+σ22,0)\left(\dfrac{\sigma_1+\sigma_2}{2},0\right)，半径 R3=σ1−σ22R_3 = \dfrac{\sigma_1 - \sigma_2}{2}
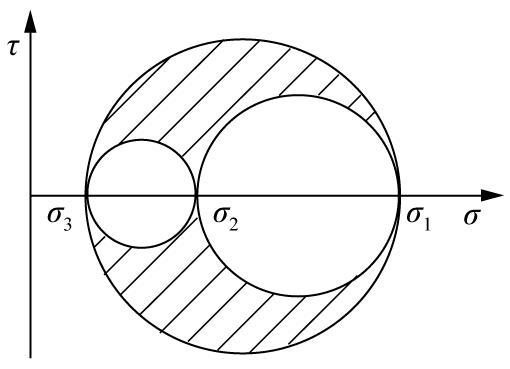
三维莫尔圆示意图
三维莫尔圆示意图

任意截面上的 (σ,τ)(\sigma, \tau) 必落在三圆围成的阴影区内。

6 平衡微分方程

考虑微元体 dx1dx2dx3\text{d}x_1 \text{d}x_2 \text{d}x_3 的力平衡，可得平衡微分方程：

∂σ11∂x1+∂σ12∂x2+∂σ13∂x3+f1=0∂σ21∂x1+∂σ22∂x2+∂σ23∂x3+f2=0∂σ31∂x1+∂σ32∂x2+∂σ33∂x3+f3=0\frac{\partial \sigma_{11}}{\partial x_1} + \frac{\partial \sigma_{12}}{\partial x_2} + \frac{\partial \sigma_{13}}{\partial x_3} + f_1 = 0 \\ \frac{\partial \sigma_{21}}{\partial x_1} + \frac{\partial \sigma_{22}}{\partial x_2} + \frac{\partial \sigma_{23}}{\partial x_3} + f_2 = 0 \\ \frac{\partial \sigma_{31}}{\partial x_1} + \frac{\partial \sigma_{32}}{\partial x_2} + \frac{\partial \sigma_{33}}{\partial x_3} + f_3 = 0

分量形式：

σij,j+fi=0\sigma_{ij,j} + f_i = 0

张量形式：

∇⋅σ+f=0\nabla \cdot \boldsymbol{\sigma} + \mathbf{f} = \mathbf{0}

引入惯性体力可得运动微分方程：

∇⋅σ+f=ρu¨\nabla \cdot \boldsymbol{\sigma} + \mathbf{f} = \rho \ddot{\boldsymbol{u}}

版权归属：Staaaaaaaaar

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)